题目内容
【题目】(1)某学习小组在探究三角形全等时,发现了下面这种典型的基本图形.如图①,已知:在△ABC中,∠BAC=90°AB=AC,直线l经过点A,BD⊥直线L,CE⊥直线L,垂足分别为点D、E.证明:①△ABD≌△CAE;②DE=BD+CE。
(2)组员小刘想,如果三个角不是直角,那结论是否会成立呢?如图②,将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线L上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.

【答案】(1)见解析;(2)成立,理由见解析.
【解析】
(1)根据同角的余角相等,可推出∠ACE=∠BAD,然后用角角边证明△ABD≌△CAE,再用全等三角形对应边相等得到BD=AE,AD=CE,从而得到DE=BD+CE;
(2)利用三角形外角性质可证得∠ABD=∠CAE,然后用角角边证明△ABD≌△CAE,同理可证明DE=BD+CE.
证明:(1)∵BD⊥直线L,CE⊥直线L,
∴∠ADB=∠CEA=90°
∴∠ACE+∠EAC=90°
又∵∠BAC=90°
∴∠BAD+∠EAC=90°,
∴∠ACE=∠BAD
在△ABD和△CAE中,
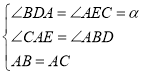
∴△ABD≌△CAE(AAS)
∴BD=AE,AD=CE
∴DE= AE+AD=BD+CE
(2)成立,理由如下:
∵∠BAE=∠BAC+∠CAE=∠ABD+∠BDA,∠BDA=∠BAC=α
∴∠CAE=∠ABD
在△ABD和△CAE中,
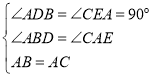
∴△ABD≌△CAE(AAS)
∴BD=AE,AD=CE
∴DE= AE+AD=BD+CE

练习册系列答案
相关题目

