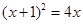题目内容
方程 kx2＋1 ＝ x－x 2 无实数根，则k ；
首先将方程整理成一元二次方程的一般形式，然后根据其无实根△＜0求得k的取值范围即可；
解：原方程整理为：（k+1）x2-x+1=0，
∵原方程无实根，
∴△=（-1）2-4（k+1）＜0，
解得：k＞-
，
故答案为：＞-
本题考查了根的判别式的知识，解题的关键是将原方程整理成一元二次方程的一般形式．
解：原方程整理为：（k+1）x2-x+1=0，
∵原方程无实根，
∴△=（-1）2-4（k+1）＜0，
解得：k＞-
，故答案为：＞-
本题考查了根的判别式的知识，解题的关键是将原方程整理成一元二次方程的一般形式．
练习册系列答案
名校通行证有效作业系列答案
相关题目
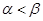，则α，β满足
2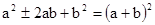
.该方法在数、式、方程等多方面应用非常广泛，如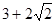
；
=
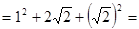
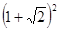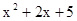
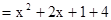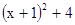等等.请你用配方法解决以下问题：
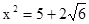；（不能出现形如
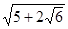的双重二次根式）
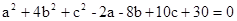，解关于x的一元二次方程
；
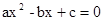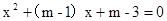总有两个不等实数根
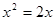的解是（ ）.（考查一元二次方程的解）
="2" 
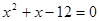
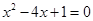（用配方法 