题目内容
【题目】已知一次函数y1=ax+c和反比例函数y2= 
的图象如图所示，则二次函数y3=ax2+bx+c的大致图象是（ ） 
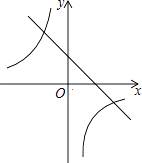
A.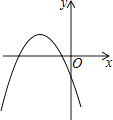
B.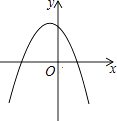
C.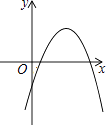
D.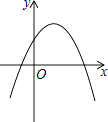
【答案】B
【解析】解：∵一次函数y1=ax+c图象过第一、二、四象限，
∴a＜0，c＞0，
∴二次函数y3=ax2+bx+c开口向下，与y轴交点在x轴上方；
∵反比例函数y2= 
的图象在第二、四象限，
∴b＜0，
∴﹣ 
＜0，
∴二次函数y3=ax2+bx+c对称轴在y轴左侧．
满足上述条件的函数图象只有B选项．
故选B．
【考点精析】利用一次函数的图象和性质和反比例函数的图象对题目进行判断即可得到答案，需要熟知一次函数是直线，图像经过仨象限；正比例函数更简单,经过原点一直线；两个系数k与b,作用之大莫小看，k是斜率定夹角,b与Y轴来相见,k为正来右上斜,x增减y增减；k为负来左下展,变化规律正相反；k的绝对值越大,线离横轴就越远；反比例函数的图像属于双曲线．反比例函数的图象既是轴对称图形又是中心对称图形．有两条对称轴：直线y=x和 y=-x．对称中心是：原点．
练习册系列答案
口算能手系列答案
相关题目
【题目】为了探究n条直线能把平面最多分成几部分,我们从最简单的情形入手:
①一条直线把平面分成2部分;
②两条直线可把平面最多分成4部分;
③三条直线可把平面最多分成7部分;
④四条直线可把平面最多分成11部分;
……
把上述探究的结果进行整理,列表分析:
直线条数 | 把平面最多 分成的部分数 | 写成和的形式 |
1 | 2 | 1+1 |
2 | 4 | 1+1+2 |
3 | 7 | 1+1+2+3 |
4 | 11 | 1+1+2+3+4 |
… | … | … |
(1)当直线条数为5时,把平面最多分成____部分,写成和的形式:______;
(2)当直线条数为10时,把平面最多分成____部分;
(3)当直线条数为n时,把平面最多分成多少部分?
