题目内容
【题目】如图,△ABC内接于⊙O,弦AD⊥AB交BC于点E,过点B作⊙O的切线交DA的延长线于点F,且∠ABF=∠ABC. 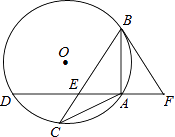
(1)求证:AB=AC;
(2)若AD=4,cos∠ABF= ![]() ,求DE的长.
,求DE的长.
【答案】
(1)证明:∵BF是⊙O的切线,
∴∠1=∠C,
∵∠ABF=∠ABC,
即∠1=∠2,
∴∠2=∠C,
∴AB=AC;
(2)解:如图,连接BD,在Rt△ADB中,∠BAD=90°,
∵cos∠ADB= ![]() ,∴BD=
,∴BD= ![]() =
= ![]() =
= ![]() =5,
=5,
∴AB=3.
在Rt△ABE中,∠BAE=90°,
∵cos∠ABE= ![]() ,∴BE=
,∴BE= ![]() =
= ![]() =
= ![]() ,
,
∴AE= ![]() =
= ![]() ,
,
∴DE=AD﹣AE=4﹣ ![]() =
= ![]() .
.
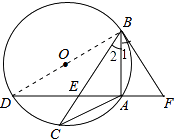
【解析】(1)由BF是⊙O的切线,利用弦切角定理,可得∠1=∠C,又由∠ABF=∠ABC,可证得∠2=∠C,即可得AB=AC;(2)首先连接BD,在Rt△ABD中,解直角三角形求出AB的长度;然后在Rt△ABE中,解直角三角形求出AE的长度;最后利用DE=AD﹣AE求得结果.
【考点精析】认真审题,首先需要了解圆周角定理(顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半),还要掌握切线的性质定理(切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径)的相关知识才是答题的关键.

【题目】下表反映的是某地区电的使用量x(千瓦时)与应交电费y(元)之间的关系,下列说法不正确的是( )
用电量x(千瓦时) | 1 | 2 | 3 | 4 | … |
应交电费y(元) | 0.55 | 1.1 | 1.65 | 2.2 | … |
A. x与y都是变量,且x是自变量,y是x的函数
B. 用电量每增加1千瓦时,电费增加0.55元
C. 当交电费20.5元时,用电量为37千瓦时
D. 若用电量为8千瓦时,则应交电费4.4元