题目内容
如图,已知A、B、C、D是⊙O上的四个点,AB=BC,BD交AC于点E,连接CD、AD.
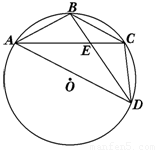
(1)求证:DB平分∠ADC;
(2)若BE=3,ED=6,求AB的长.
【答案】
(1)见解析;(2)
【解析】
试题分析:(1)由AB=BC可得弧AB=弧BC,即得∠BDC=∠ADB,从而证得结论;
(2)由弧AB=弧BC,可得∠BAC=∠ADB,再结合∠ABE=∠ABD可得△ABE∽△DBA,根据相似三角形的性质即可求得结果.
(1)∵AB=BC
∴弧AB=弧BC
∴∠BDC=∠ADB
∴DB平分∠ADC;
(2)由(1)可知弧AB=弧BC,
∴∠BAC=∠ADB
∵∠ABE=∠ABD
∴△ABE∽△DBA
∴
∵BE=3,ED=6
∴BD=9
∴AB2=BE·BD=3×9=27
∴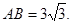
考点:圆周角定理,相似三角形的判定和性质
点评:相似三角形的判定和性质的应用是初中数学极为重要的知识,与各个知识点联系极为容易,因而是中考的热点,在各种题型中均有出现,尤其在压轴题中比较常见,难度较大,需特别注意.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,已知:DE∥BC,AB=14,AC=18,AE=10,则AD的长为( )
如图,已知:DE∥BC,AB=14,AC=18,AE=10,则AD的长为( )A、
| ||
B、
| ||
C、
| ||
D、
|
 =2,∠ADC=30°
=2,∠ADC=30° 30、如图,已知直线a,b与直线c相交,下列条件中不能判定直线a与直线b平行的是( )
30、如图,已知直线a,b与直线c相交,下列条件中不能判定直线a与直线b平行的是( )
 13、如图,已知直线AB∥CD,∠1=50°,则∠2=
13、如图,已知直线AB∥CD,∠1=50°,则∠2=