题目内容
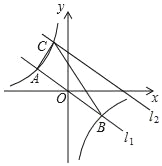
【题目】已知点 P(x,y)在第一象限,且 x+y=12,点 A(10,0)在 x 轴上,当△OPA 为直角三角形时,点 P 的坐标为_______.
【答案】(10,2)、(8,4)、(9,3).
【解析】
分情况讨论:①若O为直角顶点,则点P在y轴上,不合题意舍去; ②若A为直角顶点,则PA⊥x轴,所以点P的横坐标为10,代入y=-x+12中,得y=2,求出点P坐标为(10,2);③若P为直角顶点,可得△OPB∽△PAB,根据相似三角形的性质求出P点横坐标,进而得到P点坐标.
分情况讨论:
①若O为直角顶点,则点P在y轴上,不合题意舍去;
②若A为直角顶点,则PA⊥x轴,所以点P的横坐标为10,代入y=-x+12中,得y=2,
所以点P坐标(10,2);
③若P为直角顶点,可得△OPB∽△PAB,
∴![]() ,
,
∴PB2=OBAB,
∴(-x+12)2=x(10-x),
解得x=8或9,
∴点P坐标(8,4)或(9,3),
∴当△OPA为直角三角形时,点P的坐标为(10,2)、(8,4)、(9,3),
故答案为:(10,2)、(8,4)、(9,3).

练习册系列答案
相关题目