题目内容
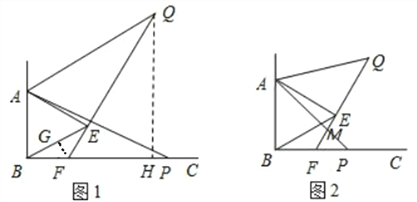
【题目】如图,已知∠ABC=90°,△ABE是等边三角形,点P为射线BC上任意一点(点P与点B不重合),连接AP,将线段AP绕点A逆时针旋转60°得到线段AQ,连接QE并延长交射线BC于点F.
(1)如图,当BP=BA时,∠EBF=______°,猜想∠QFC =______°;
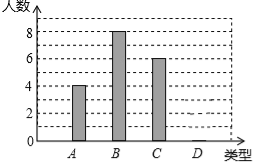
(2)如图,当点P为射线BC上任意一点时,猜想∠QFC的度数,并加以证明.
(3)已知线段AB=![]() ,设BP=x,点Q到射线BC的距离为y,求y关于x的函数关系式.
,设BP=x,点Q到射线BC的距离为y,求y关于x的函数关系式.
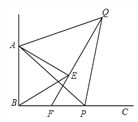
【答案】(1)∠EBF=30°; ∠QFC=60°;(2)∠QFC=60°.(3)![]() (x>0).
(x>0).
【解析】试题分析:(1)∠EBF与∠ABE互余,而∠ABE=60°,即可求得∠EBF的度数;利用观察法,或量角器测量的方法即可求得∠QFC的度数;
(2)根据三角形的外角等于不相邻的两内角的和,证明∠BAP=∠EAQ,进而得到△ABP≌△AEQ,证得∠AEQ=∠ABP=90°,则∠BEF=180°-∠AEQ-∠AEB=180°-90°-60°=30°,∠QFC=∠EBF+∠BEF;
(3)过点F作FG⊥BE于点G,过点Q作QH⊥BC,根据△ABP≌△AEQ得到:设QE=BP=x,则QF=QE+EF=x+2.点Q到射线BC的距离y=QH=sin60°×QF=![]() (x+2),即可求得函数关系式.
(x+2),即可求得函数关系式.
试题解析:(1)∵∠ABC=90°,∠BAE=60°,
∴∠EBF=30°;
则猜想:∠QFC=60°;
(2)∠QFC=60°.
∵∠BAP=∠BAE+∠EAP=60°+∠EAP,∠EAQ=∠QAP+∠EAP=60°+∠EAP,
∴∠BAP=∠EAQ
在△ABP和△AEQ中,
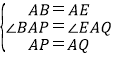 ,
,
∴△ABP≌△AEQ (SAS)
∴∠AEQ=∠ABP=90°
∴∠BEF=180°-∠AEQ-∠AEB=180°-90°-60°=30°,
∴∠QFC=∠EBF+∠BEF=30°+30°=60°;
(3)在图1中,过点F作FG⊥BE于点G,过点Q作QH⊥BC于点H,
∵△ABE是等边三角形,
∴BE=AB=![]() ,
,
由(1)得∠EBF=30°,在Rt△BGF中,![]()
∴FG=2,BF=4,∴EF=BF=4,
∵△ABP≌△AEQ,∴QE=PB=x,∴QF=QE+EF=x+4,
由(2)得∠QFC=60°,∴在Rt△QHF中,∠FQH=30°
![]()
即y关于x的函数关系式是:![]() (x>0)
(x>0)
.