题目内容
如图,在边长为24cm的正方形纸片ABCD上,剪去图中阴影部分的四个全等的等腰直角三角形,再沿图中的虚线折起,折成一个长方体形状的包装盒(A、B、C、D四个顶点正好重合于上底面上一点)。已知E、F在AB边上,是被剪去的一个等腰直角三角形斜边的两个端点,设AE=BF=x(cm).

(1)若折成的包装盒恰好是个正方体,试求这个包装盒的体积V;
(2)某广告商要求包装盒的表面(不含下底面)面积S最大,试问x应取何值?S最大值是多少?

(1)若折成的包装盒恰好是个正方体,试求这个包装盒的体积V;
(2)某广告商要求包装盒的表面(不含下底面)面积S最大,试问x应取何值?S最大值是多少?
(1)432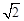 cm3;(2)当x=8时,S取得最大值384cm2.
cm3;(2)当x=8时,S取得最大值384cm2.
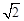 cm3;(2)当x=8时,S取得最大值384cm2.
cm3;(2)当x=8时,S取得最大值384cm2.试题分析:(1)根据已知得出这个正方体的底面边长a=
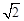 x,EF=
x,EF=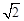 a=2x,再利用AB=24cm,求出x即可得出这个包装盒的体积V;
a=2x,再利用AB=24cm,求出x即可得出这个包装盒的体积V;(2)利用已知表示出包装盒的表面,从而利用函数最值求出即可.
试题解析:(1)根据题意,知这个正方体的底面边长a=
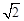 x,EF=
x,EF=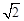 a=2x,
a=2x,∴x+2x+x=24,解得:x="6." 则 a=6
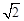 .
.∴V=a3=(6
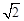 )3=432
)3=432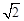 (cm3).
(cm3).(2)设包装盒的底面边长为acm,高为hcm,则a=
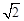 x,
x,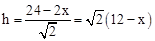 ,
,∴S=4ah+a2=
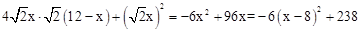 .
.∵0<x<12,∴当x=8时,S取得最大值384cm2.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
 与x轴交于A、B两点,与y轴交于C点,四边形OBHC为矩形,CH的延长线交抛物线于点D(5,2),连结BC、AD.
与x轴交于A、B两点,与y轴交于C点,四边形OBHC为矩形,CH的延长线交抛物线于点D(5,2),连结BC、AD.
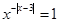 ,则x=1或x=3;(3)若函数
,则x=1或x=3;(3)若函数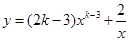 是关于x的反比例函数,则
是关于x的反比例函数,则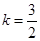 ;(4)已知二次函数
;(4)已知二次函数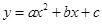 ,且a>0,a-b+c<0,则
,且a>0,a-b+c<0,则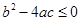 。其中,正确的命题有( )个.
。其中,正确的命题有( )个. (
( >0)的对称轴为直线
>0)的对称轴为直线 ,且经过点(-3,
,且经过点(-3,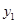 ),(4,
),(4,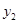 ),试比较
),试比较