题目内容
在平面直角坐标系中,点O是坐标原点、已知等腰梯形OABC,OA∥BC,点A(4,0),BC=2,等腰梯形OABC的高是1,且点B、C都在第一象限.(1)请画出一个平面直角坐标系,并在此坐标系中画出等腰梯形OABC;
(2)直线y=-
| 1 |
| 5 |
| 6 |
| 5 |
| 1 |
| 5 |
| 6 |
| 5 |
分析:(1)求出梯形的各个顶点的坐标即可;
(2)利用待定系数法即可求得AB的解析式,进而求得P的坐标,即可求解.
(2)利用待定系数法即可求得AB的解析式,进而求得P的坐标,即可求解.
解答: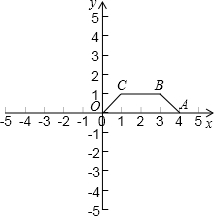 解:(1)画平面直角坐标系.
解:(1)画平面直角坐标系.
画等腰梯形OABC(其中点B(3,1)、点C(1,1)).
(2)依题意得,B(3,1)
设直线AB:y=kx+b,
将A(4,0)B(3,1)代入得
∴直线AB:y=-x+4.
法一:
解方程组
得x=
,即p=
,
∵函数y=-
x+
随着x的增大而减小,
∴要使n>q,须m<p,
∴当n>q时,m的取值范围是m<
.
法二:
解方程组
得
∴p=
,q=
,
∴点M(m,n)在直线y=-
x+
上
∴n=-
m+
,
∵n>q
∴-
m+
>
,
∴m<
,
∴当n>q时,m的取值范围是m<
 解:(1)画平面直角坐标系.
解:(1)画平面直角坐标系.画等腰梯形OABC(其中点B(3,1)、点C(1,1)).
(2)依题意得,B(3,1)
设直线AB:y=kx+b,
将A(4,0)B(3,1)代入得
|
∴直线AB:y=-x+4.
法一:
解方程组
|
| 7 |
| 2 |
| 7 |
| 2 |
∵函数y=-
| 1 |
| 5 |
| 6 |
| 5 |
∴要使n>q,须m<p,
∴当n>q时,m的取值范围是m<
| 7 |
| 2 |
法二:
解方程组
|
|
| 7 |
| 2 |
| 1 |
| 2 |
∴点M(m,n)在直线y=-
| 1 |
| 5 |
| 6 |
| 5 |
∴n=-
| 1 |
| 5 |
| 6 |
| 5 |
∵n>q
∴-
| 1 |
| 5 |
| 6 |
| 5 |
| 1 |
| 2 |
∴m<
| 7 |
| 2 |
∴当n>q时,m的取值范围是m<
| 7 |
| 2 |
点评:此题把一次函数与等腰梯形相结合,考查了同学们综合运用所学知识的能力,是一道综合性较好的题目.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
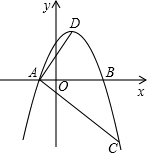 坐标原点.A、B两点的横坐标分别是方程x2-4x-12=0的两根,且cos∠DAB=
坐标原点.A、B两点的横坐标分别是方程x2-4x-12=0的两根,且cos∠DAB=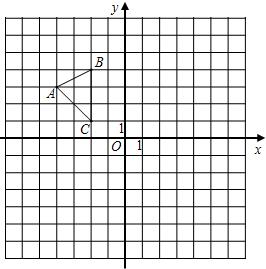 18、在平面直角坐标系中,把一个图形先绕着原点顺时针旋转的角度为θ,再以原点为位似中心,相似比为k得到一个新的图形,我们把这个过程记为【θ,k】变换.例如,把图中的△ABC先绕着原点O顺时针旋转的角度为90°,再以原点为位似中心,相似比为2得到一个新的图形△A1B1C1,可以把这个过程记为【90°,2】变换.
18、在平面直角坐标系中,把一个图形先绕着原点顺时针旋转的角度为θ,再以原点为位似中心,相似比为k得到一个新的图形,我们把这个过程记为【θ,k】变换.例如,把图中的△ABC先绕着原点O顺时针旋转的角度为90°,再以原点为位似中心,相似比为2得到一个新的图形△A1B1C1,可以把这个过程记为【90°,2】变换.