题目内容
【题目】问题呈现
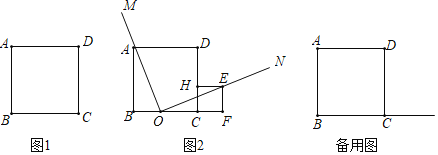
如图,四边形ABCD是矩形,AB=20,BC=10,以CD为一边向矩形外部作等腰直角△GDC,∠G=90°,点M在线段AB上,且AM=a,点P沿折线AD-DG运动,点Q沿折线BC-CG运动(与点G不重合),在运动过程中始终保持线段PQ//AB.设PQ与AB之间的距离为x.
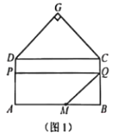
(1)若a=12.①如图1,当点P在线段AD上时,若四边形AMQP的面积为48,则x的值为_________;
②在运动过程中,求四边形AMQP的最大面积;
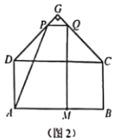
(2)如图2,若点P在线段DG上时,要使四边形AMQP的面积始终不小于50,求a的取值范围.


【答案】(1)①3,②x=13时,S四AMQP最大值=169;(2)5≤a≤20.
【解析】
(1)①P在线段AD上,PQ=AB=20,AP=x,AM=12,由梯形面积公式得出方程,解方程即可;
②分点P在AD上、点P在DG上,两种情况,根据梯形的面积以及二次函数的性质分别求出两种情况下面积的最大值,比较即可得;
(2)P在DG上,则10≤x≤20,AM=a, PQ=40-2x,可得S四边形AMQP=![]() ,得出对称轴为:x=
,得出对称轴为:x=![]() ,继而得出10≤
,继而得出10≤![]() ≤15,对称轴在10到15之间,再根据10≤x≤20,二次函数图象的开口向下,可知当x=20时,S最小,得出
≤15,对称轴在10到15之间,再根据10≤x≤20,二次函数图象的开口向下,可知当x=20时,S最小,得出![]() ≥50,求出a≥5,即可得出答案.
≥50,求出a≥5,即可得出答案.
(1)①P在线段AD上,PQ=AB=20,AP=x,AM=a=12,
S四边形AMQP=![]() ,
,
解得x=3,
故答案为:3;
②当P在AD上时,P到D点时四边形AMQP的面积最大,此时为直角梯形,
∴0≤x≤10时,S四边形AMQP=![]()
![]() ,
,
当x=10时,S四边形AMQP最大值=160;
当P在DG上,即10≤x≤20,四边形AMQP为不规则梯形,
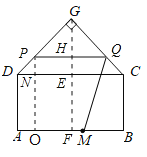
如图,作PO⊥AB于M,交CD于N,作GE⊥CD于E,交AB于F,交PQ于点H,
则PO=x,PN=x-10,EF=BC=10,
∵△GDC是等腰直角三角形,
∴DE=CE,GE=![]() CD=10,
CD=10,
∴GF=GE+EF=20,∴GH=20-x,
由题意,PQ//CD,
∴△GPQ∽△GDC,
∴PQ:DC=GH:GE,
即PQ:20=(20-x):10,
∴PQ=40-2x,
∴S梯形AMQP=![]() =-x2+26x=-(x-13)2+169,
=-x2+26x=-(x-13)2+169,
∴当x=13时,四边形AMQP的面积最大为169,
综上:x=13时,S四边形AMQP最大值=169;
(2)P在DG上,则10≤x≤20,AM=a,由(1)知:PQ=40-2x,
S四边形AMQP=![]() ,
,
对称轴为:x=![]() ,开口向下,
,开口向下,
∵0≤a≤20,
∴10≤![]() ≤15,对称轴在10到15之间,
≤15,对称轴在10到15之间,
∵10≤x≤20,二次函数图象的开口向下,
∴当x=20时,S最小,
∴![]() ≥50,
≥50,
∴a≥5,
综上所述:5≤a≤20.

 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案【题目】某宾馆有若干间标准房,当标准房的价格为200元时,每天入住的房间数为60间,经市场调查表明,该宾馆每间标准房的价格在170~240元之间(含170元,240元)浮动时,每天入住的房间数![]() (间)与每间标准房的价格
(间)与每间标准房的价格![]() (元)的数据如下表:
(元)的数据如下表:
| … | 190 | 200 | 210 | 220 | … |
| … | 65 | 60 | 55 | 50 | … |

(1)根据所给数据在坐标系中描出相应的点,并画出图象.
(2)求![]() 关于
关于![]() 的函数表达式、并写出自变量
的函数表达式、并写出自变量![]() 的取值范围.
的取值范围.
(3)设客房的日营业额为![]() (元).若不考虑其他因素,问宾馆标准房的价格定为多少元时.客房的日营业额最大?最大为多少元?
(元).若不考虑其他因素,问宾馆标准房的价格定为多少元时.客房的日营业额最大?最大为多少元?