题目内容
（2002•大连）已知：有公共端点的线段AB、BC（如图），求作：⊙O，使它经过点A、B、C（要求：尺规作图，不写作法，保留作图痕迹）．
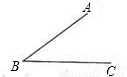
【答案】分析：此题求作的实际是△ABC的外接圆，由于三角形的外心是三角形三边中垂线的交点，所以只需作出AB、BC的垂直平分线，两条中垂线的交点即为所求圆的圆心O．
解答：解：如图．
作法：①以A、B为圆心，大于
AB长为半径作弧，交于G、H，连接GH；
②以B、C为圆心，大于
BC长为半径作弧，交于M、N，连接MN；
③直线GH、MN交于点O，连接OB；
④以O为圆心，OB长为半径作圆．
结论：⊙O即为所求作的圆．
点评：理解三角形的外心是三边中垂线的交点是解答此题的关键．
解答：解：如图．
作法：①以A、B为圆心，大于
AB长为半径作弧，交于G、H，连接GH；②以B、C为圆心，大于
BC长为半径作弧，交于M、N，连接MN；③直线GH、MN交于点O，连接OB；
④以O为圆心，OB长为半径作圆．
结论：⊙O即为所求作的圆．
点评：理解三角形的外心是三边中垂线的交点是解答此题的关键．
练习册系列答案
相关题目
