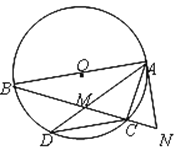
题目内容
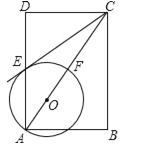
【题目】如图,△ABC内接于⊙O,AB为⊙O直径,AC=CD,连接AD交BC于点M,延长MC到N,使CN=CM.
(1)判断直线AN是否为⊙O的切线,并说明理由;
(2)若AC=10,tan∠CAD=![]() ,求AD的长.
,求AD的长.
【答案】(1)是 (2)16
【解析】(1)由MC=CN,且得出AC垂直于MN,则△AMN是等腰三角形,所以∠CAN=∠DAC,再由AC=DC,则∠D=∠DAC,根据同弧所对的圆周角相等得出∠B=∠D,从而得出∠B=∠NAC,即可得出∠BAN=90°;
(2)等腰三角形ACD中,两腰AC=CD=10,且已知底角正切值,过点C作CE⊥AD,底边长AD可以求出来.
(1)直线AN是⊙O的切线,理由是:
∵AB为⊙O直径,
∴∠ACB=90°,
∴AC⊥BC,
∵CN=CM,
∴∠CAN=∠DAC,
∵AC=CD,
∴∠D=∠DAC,
∵∠B=∠D,
∴∠B=∠NAC,
∵∠B+∠BAC=90°,
∴∠NAC+∠BAC=90°,
∴OA⊥AN,
又∵点A在⊙O上,
∴直线AN是⊙O的切线;
(2)过点C作CE⊥AD,
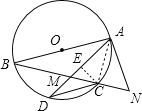
∵tan∠CAD=![]() ,
,
∴![]() ,
,
∵AC=10,
∴设CE=3x,则AE=4x,
在Rt△ACE中,根据勾股定理,CE2+AE2=AC2,
∴(3x)2+(4x)2=100,
解得x=2,
∴AE=8,
∵AC=CD,
∴AD=2AE=2×8=16.

练习册系列答案
相关题目