Question

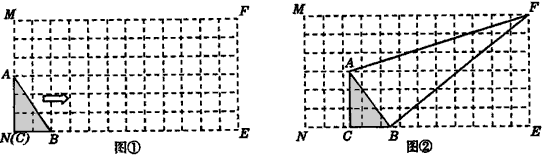
如图①，在6×12的方格纸MNEF中，每个小正方形的边长都是1。Rt△ABC的顶点C与N重合，两直角边AC、BC分别在加MN、NE上，且AC=3，BC=2．现Rt△ABC以每秒1个单位长的速度向右平移，当点B移动至点E时，Rt△ABC停止移动。     
（1）请你在答题卡所附的6×12的方格纸①中，画出Rt△ABC向右平移4秒时所在的图形；    
（2）如图②，在Rt△ABC向右平移的过程中，△ABF能否成为直角三角形？如果能，请求出相应的时间t，如果不能，请简要说明理由；     
（3）如图②，在Rt△ABC向右平移的过程中（不包括平移的开始与结束时刻），其外接圆与直线AF、直线BF分别有哪几种位置关系？请直接写出这几种位置关系及所对应的时间t的范围（不必说理）

Answer 1

解：
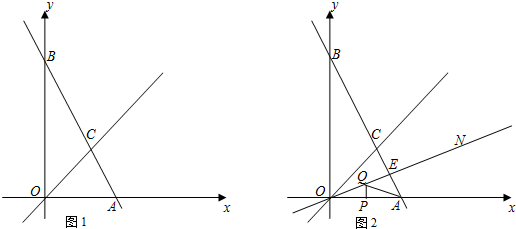
（1）
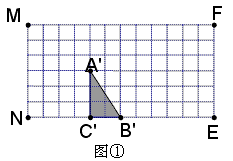
（2）能。如方格纸②所示。设Rt△ABC向右平移t秒，
则NC=t ，BE=10-t，AH=12-t 。
在Rt△ABC中，由勾股定理得： AB²=CB²+CA²=2²+3²=13 。
同理可得： BF²=BE²+EF²=（10-t）²+6²
AF²=AH²+FH²=3²+（12-t）²
当AB²+BF²=AF²时，由勾股定理的逆定理得，∠ABF=90°
即△ABF为Rt△。此时由AB²+BF²=AF²
得13+（10-t）²+6²=3²+（12-t）²   解得t=1。
当AB²+AF²=BF²时，由勾股定理的逆定理得：∠BAF=90°
即△ABF为Rt△。此时由AB²+AF²=BF²
得13+3²+（12-t）² = （10-t）²+6² 。解得t=7.5
(3)依题意得：当t=7.5时, 直线AF与Rt△ABC的外接圆相切；
当0<t<7.5或7.5<t<10时，直线AF与Rt△ABC的外接圆相交；
当t=1时, 直线BF与Rt△ABC的外接圆相切；
当0<t<1或1<t<10时，直线BF与Rt△ABC的外接圆相交。