题目内容
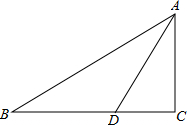（2012•重庆模拟）如图，在Rt△ABC中，∠C=90°，∠B=30°，∠ADC=60°，BD=10，求AC的长．分析：利用三角形的外角和定理和给出的已知数据可求出∠BAD=30°，所以△ABD为等腰三角形，即AD=BD=10，再利用含60°角的直角三角形可解，进而求出AC的长．
解答：解：∵∠B=30°，∠ADC=60°，
∴∠BAD=∠ADC-∠B=30°，
∴AD=BD=10，
∵∠C=90°，
∴sin60°=
=
，
∴AC=AD•
=5
．
∴∠BAD=∠ADC-∠B=30°，
∴AD=BD=10，
∵∠C=90°，
∴sin60°=
| AC |
| AD |
| ||
| 2 |
∴AC=AD•
| ||
| 2 |
| 3 |
点评：本题考查了三角形的外角和定理、等腰三角形的判定和性质以及解直角三角形的有关知识．属于基础题目．
练习册系列答案
相关题目