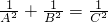题目内容

一圆内接三角形的边长分别是20、21和29，这三角形把圆分成四个区域，设非三角形区域面积分别是A、B和C，并且C是最大，如图所示，那么（）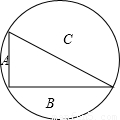

A．A+B=C
B．A+B+210=C
C．A²+B²=C²
D．

【答案】分析：根据勾股定理的逆定理得到三角形是直角三角形，再根据圆周角定理的推论，知直角三角形的斜边是直径，从而A+B+直角三角形的面积=C，从而判断．
解答：解：∵20²+21²=29²，
∴三角形是直角三角形，
∴直角三角形的斜边是直径，
∴A+B+直角三角形的面积=C，
即A+B+210=C．
故选B．
点评：此题主要是圆周角定理及其推论的运用．注意：90°的圆周角所对的弦是直径．

练习册系列答案

68所名校图书小升初高分夺冠真卷系列答案

伴你成长周周练月月测系列答案

小升初金卷导练系列答案

相关题目

一圆内接三角形的边长分别是20、21和29，这三角形把圆分成四个区域，设非三角形区域面积分别是A、B和C，并且C是最大，如图所示，那么（　　）

平面直角坐标系中,M(36,0),⊿OMN是等腰直角三角形,∠ONM=90°

(1) 直接写出N的坐标;
(2) 正方形ABCD是⊿OMN的内接正方形,求正方形边长;
(3) 在（2）的情况下，点P为线段AB上一点,以P为圆心,PB为半径的圆交线段AD于点E.当B,E,N在一条直线上时,求⊙P半径;
(4) 在(3)的情况下,线段CD上取点F,使∠EBF=45°,连结EF,判断直线EF与⊙P是否相切.若是,写出推理过程;若不是,说明理由.

平面直角坐标系中,M(36,0),⊿OMN是等腰直角三角形,∠ONM=90°

(1) 直接写出N的坐标;

(2) 正方形ABCD是⊿OMN的内接正方形,求正方形边长;

(3) 在（2）的情况下，点P为线段AB上一点,以P为圆心,PB为半径的圆交线段AD于点E.当B,E,N在一条直线上时,求⊙P半径;

(4) 在(3)的情况下,线段CD上取点F,使∠EBF=45°,连结EF,判断直线EF与⊙P是否相切.若是,写出推理过程;若不是,说明理由.

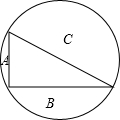一圆内接三角形的边长分别是20、21和29，这三角形把圆分成四个区域，设非三角形区域面积分别是A、B和C，并且C是最大，如图所示，那么

A.
A+B=C
B.
A+B+210=C
C.
A²+B²=C²
D.
$数学公式$

一圆内接三角形的边长分别是20、21和29，这三角形把圆分成四个区域，设非三角形区域面积分别是A、B和C，并且C是最大，如图所示，那么

试题分类