题目内容
(2012•东城区二模)阅读并回答问题:
小亮是一位刻苦学习、勤于思考、勇于创新的同学.一天他在解方程x2=-1时,突发奇想:x2=-1在实数范围内无解,如果存在一个数i,使 i2=-1,那么当x2=-1时,有x=±i,从而x=±i是方程x2=-1的两个根.
据此可知:(1)i可以运算,例如:i3=i2•i=-1×i=-i,则i4=
(2)方程x2-2x+2=0的两根为
小亮是一位刻苦学习、勤于思考、勇于创新的同学.一天他在解方程x2=-1时,突发奇想:x2=-1在实数范围内无解,如果存在一个数i,使 i2=-1,那么当x2=-1时,有x=±i,从而x=±i是方程x2=-1的两个根.
据此可知:(1)i可以运算,例如:i3=i2•i=-1×i=-i,则i4=
1
1
,i2011=-i
-i
,i2012=1
1
;(2)方程x2-2x+2=0的两根为
1+i或1-i
1+i或1-i
(根用i表示).分析:(1)根据 i2=-1可将i4化为i2•i2;i2011=(i2)1005•i;i2012=(i2)1006•i进行计算即可;
(2)先根据-1=i2求出△的值,再由公式法求出x的值即可.
(2)先根据-1=i2求出△的值,再由公式法求出x的值即可.
解答:解:(1)∵i2=-1,
∴i4=i2•i2=(-1)×(-1)=1;
i2011=(i2)1005•i=(-1)1005•i=-i;
i2012=(i2)1006•i=(-1)1006•i=i.
故答案为:1,-i,1.
(2)∵△=(-2)2-4×1×2=-4,i2=-1,
∴△=4i2,
∴方程x2-2x+2=0的两根为x=
=1±i,即x=1+i或x=1-i.
故答案为:1+i或1-i.
∴i4=i2•i2=(-1)×(-1)=1;
i2011=(i2)1005•i=(-1)1005•i=-i;
i2012=(i2)1006•i=(-1)1006•i=i.
故答案为:1,-i,1.
(2)∵△=(-2)2-4×1×2=-4,i2=-1,
∴△=4i2,
∴方程x2-2x+2=0的两根为x=
| 2±2i |
| 2×1 |
故答案为:1+i或1-i.
点评:本题考查的是用公式法求一元二次方程的根,先根据题中所给的材料记住i2=-1是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
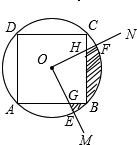 (2012•东城区二模)如图,正方形ABCD内接于⊙O,⊙O的半径为2,以圆心O为顶点作∠MON,使∠MON=90°,OM、ON分别与⊙O交于点E、F,与正方形ABCD的边交于点G、H,则由OE、OF、
(2012•东城区二模)如图,正方形ABCD内接于⊙O,⊙O的半径为2,以圆心O为顶点作∠MON,使∠MON=90°,OM、ON分别与⊙O交于点E、F,与正方形ABCD的边交于点G、H,则由OE、OF、
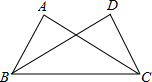 (2012•东城区二模)已知:如图,∠ABC=∠DCB,BD、CA分别是∠ABC、∠DCB的平分线.
(2012•东城区二模)已知:如图,∠ABC=∠DCB,BD、CA分别是∠ABC、∠DCB的平分线.