题目内容
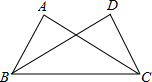 (2012•东城区二模)已知:如图,∠ABC=∠DCB,BD、CA分别是∠ABC、∠DCB的平分线.
(2012•东城区二模)已知:如图,∠ABC=∠DCB,BD、CA分别是∠ABC、∠DCB的平分线.求证:AB=DC.
分析:根据角平分线性质和已知求出∠ACB=∠DBC,根据ASA推出△ABC≌△DCB,根据全等三角形的性质推出即可.
解答:证明:∵AC平分∠BCD,BD平分∠ABC,
∴∠DBC=
∠ABC,∠ACB=
∠DCB,
∵∠ABC=∠DCB,
∴∠ACB=∠DBC,
∵在△ABC与△DCB中,
,
∴△ABC≌△DCB,
∴AB=DC.
∴∠DBC=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠ABC=∠DCB,
∴∠ACB=∠DBC,
∵在△ABC与△DCB中,
|
∴△ABC≌△DCB,
∴AB=DC.
点评:本题考查了全等三角形的性质和判定和角平分线性质的应用,关键是推出△ABC≌△DCB,题目比较好,难度适中.

练习册系列答案
相关题目
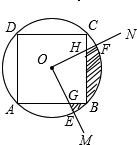 (2012•东城区二模)如图,正方形ABCD内接于⊙O,⊙O的半径为2,以圆心O为顶点作∠MON,使∠MON=90°,OM、ON分别与⊙O交于点E、F,与正方形ABCD的边交于点G、H,则由OE、OF、
(2012•东城区二模)如图,正方形ABCD内接于⊙O,⊙O的半径为2,以圆心O为顶点作∠MON,使∠MON=90°,OM、ON分别与⊙O交于点E、F,与正方形ABCD的边交于点G、H,则由OE、OF、