题目内容
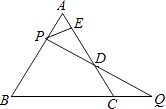
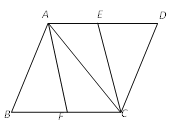
【题目】如图,在□ABCD中,E、F分别是AD、BC的中点,连接AC、CE、AF.
(1)求证△ABF ≌ △CDE;
(2)若AB=AC,求证四边形AFCE是矩形.
【答案】(1)证明见解析;(2)证明见解析
【解析】试题分析:(1)、根据平行四边形的性质得出AB=CD,AD=BC,∠B=∠D,根据中点的性质得出BF=DE,最后根据SAS判定出三角形全等;(2)、首先根据全等以及中点的性质得出四边形AFCE为平行四边形,根据等腰三角形的性质得出AF⊥BC,从而得出矩形.
试题解析:(1)、∵ 四边形ABCD是平行四边形,∴ AB=CD,AD=BC,∠B=∠D.
∵ E、F分别是AD、BC的中点, ∴ DE=AE= ![]() AD, BF=CF=
AD, BF=CF= ![]() BC.∴ BF=DE,CF=AE.
BC.∴ BF=DE,CF=AE.
∴ △ABF≌△CDE(SAS).
(2)∵△ABF≌△CDE(SAS), ∴ AF=CE. 又∵CF=AE,
∴四边形AFCE是平行四边形. ∵AB=AC, F分别是BC的中点, ∴AF⊥BC.
即∠AFC=90°. ∴四边形AFCE是矩形.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
【题目】王华、张伟两位同学分别将自己10次数学自我检测的成绩绘制成如下统计图:
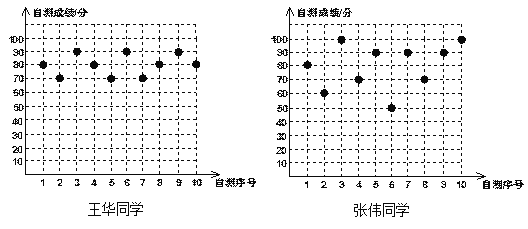
(1)根据上图中提供的数据列出如下统计表:
平均成绩(分) | 中位数(分) | 众数(分) | 方差(S2) | |
王华 | 80 | b | 80 | d |
张伟 | a | 85 | c | 260 |
则a= ,b= ,c= ,d= ,
(2)将90分以上(含90分)的成绩视为优秀,则优秀率高的是 .
(3)现在要从这两个同学选一位去参加数学竞赛,你可以根据以上的数据给老师哪些建议?