Question

【题目】如图，分别以Rt△ABC的斜边AB、直角边AC为边向外作等边△ABD和△ACE，F为AB中点，连接DF、EF，DE、EF与AC交于点O，DE与AB交于点G，连接OG，若∠BAC=30°，下列结论：①△DBF≌△EFA；②AD=AE；③EF⊥AC；④AD=4AG；⑤△AOG与△EOG的面积比为1：4．其中正确的结论的序号是_____．

Answer 1

【答案】①③④

【解析】

根据等边三角形的性质求出∠EAC=60°，AE=AC，求出BC=AF，根据SAS证△ABC≌△EFA，推出FE=AB，∠AEF=∠BAC=30°，求出∠AOE=90°，即可判断③；求出AD=BD，BF=AF，∠DFB=∠EAF，∠BDF=∠AEF，根据AAS证△DBF≌△EFA，即可判断①；得出四边形ADFE为平行四边形，推出AG=AF，AG=AB，求出AD=AB，推出AD=4AG，即可判断④；求出∠FAE=90°，∠AFE＜90°，推出EF＞AE，即可判断②；根据平行四边形性质得出AG=GF，推出S三角形AGOS三角形GOF，设AG=1，则AF=2，AB=4，BC=2，由勾股定理求出AC=2，求出AO=OC，由勾股定理求出OE=3，得出△GOF和△EGO的面积比是1：3，即可判断⑤．

解：∵△ACE是等边三角形，

∴∠EAC=60°，AE=AC，

∵∠BAC=30°，

∴∠FAE=∠ACB=90°，AB=2BC，

∵F为AB的中点，

∴AB=2AF，

∴BC=AF，

在△ABC和△EFA中

,

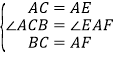∴△ABC≌△EFA（SAS），

∴FE=AB，∠AEF=∠BAC=30°，

∠AOE=180°-30°-60°=90°，

∴EF⊥AC，∴③正确，

∵AD=BD，BF=AF，

∴∠DFB=90°，∠BDF=30°，

∵∠FAE=∠BAC+∠CAE=90°，

∴∠DFB=∠EAF，

∵EF⊥AC，

∴∠AEF=30°，

∴∠BDF=∠AEF，

在△DBF和△EFA中

,

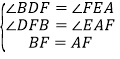∴△DBF≌△EFA（AAS），∴①正确；

∴AE=DF，

∵FE=AB，

∴四边形ADFE为平行四边形，

∴AG=AF，AG=AB，

∵AD=AB，

则AD=4AG，∴④正确；

∵四边形ADFE为平行四边形，

∴AD=EF，

∵∠FAE=90°，∠AFE＜90°，

∴EF＞AE，

即AD＞AE，∴②错误；

∵四边形ADFE为平行四边形，

∴AG=GF，

∴S三角形AGO=S三角形GOF，

设AG=1，则AF=2，AB=4，BC=2，由勾股定理得：AC=2，

∠CAE=60°，∠AEF=∠CAB=30°，

∴∠COE=30°+60°=90°=∠AOE，

∵AE=CE，

∴AO=OC，

在等边三角形ACE中，AE=AC=2，AO=OC=，

由勾股定理得：OE==3，

∵△GOF的边OF和△EGO的边OE上的高相等，

∴△GOF和△EGO的面积比是1：3，

即△AOG与△EOG的面积比为1：3，∴⑤错误；

正确的有①③④，

故答案为：①③④．