题目内容
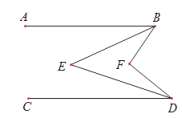
【题目】如图,AB∥CD,BE,DE分别平分∠ABF,∠FDC,试问∠E与∠F之间的数量关系如何?请说明理由.
【答案】∠F=2∠E
【解析】试题分析:过点E作直线EM∥AB,过点N作直线FN∥AB,由平行线的性质可得∠BED=∠ABE+∠CDE,∠BFD=∠ABF+∠CDF,再根据角平分线的性质,即可得到∠BED和∠BED的关系.
试题解析:解:∠BFD=2∠BED.理由如下:
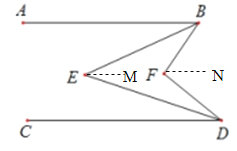
过点E作直线EM∥AB,过点N作直线FN∥AB.
又∵AB∥CD,∴EM∥CD,FN∥CD(平行于同一直线的两直线互相平行),∴∠ABE=∠BEM,∠CDE=∠DEM(两直线平行,内错角相等),∴∠BED=∠BEM+∠DEM=∠ABE+∠CDE.
同理可得:∠BFD=∠ABF+∠CDF.
∵BE,DE分别平分∠ABF,∠FDC,∴∠ABF=2∠ABE,∠CDF=2∠CDE(角平分线定义)
∴∠BFD=2∠BED.

练习册系列答案
相关题目