Question

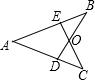
如图，在△ABC中，AB=AC，点D、E分别是AB、AC的中点，点F是BE、CD的交点．请写出图中两组全等的三角形，并选出其中一组加以证明．（要求：写出证明过程中的重要依据）

Answer 1

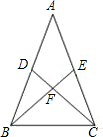
△ABE≌△ACD，∠FAE=∠EAD或△BFD≌△CFE（写出两个即可）
（1）选△ABE≌△ACD．
证明：∵点D，E分别是AB，AC的中点，
∴AD=

1

2

AB，AE=

1

2

AC．
又∵AB=AC，
∴AD=AE．
在△ABE和△ACD中，

AB=AC ∠BAE=∠CAD AE=AD.

，
∴△ABE≌△ACD（SAS）．

（2）选△BCD≌△CBE．
证明：∵AB=AC，∴∠ABC=∠ACB（等边对等角）．
∵点D，E分别是AB，AC的中点，
∴BD=

1

2

AB，CE=

1

2

AC．
∴BD=CE．
在△BCD和△CBE中，

BD=CE ∠ABC=∠ACB BC=CB

，
∴△BCD≌△CBE（SAS）．

（3）选△BFD≌△CFE．
方法一：
证明：∵点D，E分别是AB，AC的中点，
∴AD=

1

2

AB，AE=

1

2

AC
又∵AB=AC，∴AD=AE
在△ABE和△ACD中，

AB=AC ∠BAE=∠CAD AE=AD

∴△ABE≌△ACD（SAS）
∴∠ABE=∠ACD（全等三角形对应角相等）
∵点D，E分别是AB，AC的中点，∴BD=

1

2

AB，CE=

1

2

AC
∵AB=AC，∴BD=CE
在△BFD和△CFE中，

∠ABE=∠ACD ∠DFB=∠EFC(对顶角相等) BD=CE.

M（m，0）
方法二：
证明：∵AB=AC，
∴∠ABC=∠ACB（等边对等角）．
∵点D，E分别是AB，AC的中点，
∴BD=

1

2

AB，CE=

1

2

AC．
∴BD=CE．
在△BCD和△CBE中，

BD=CE ∠ABC=∠ACB BC=CB

，
∴△BCD≌△CBE（SAS）．
∴∠BDC=∠CEB（全等三角形对应角相等）．
在△BFD和△CFE中，

∠BDC=∠CEB ∠DFB=∠EFC(对顶角相等) BD=CE.

，
∴△BFD≌△CFE（AAS）．