题目内容
字母系数的二元一次方程组(1)当a为何值时,方程组
|
(2)当m为何值时,方程组
|
分析:(1)根据加减消元的思想,消掉常数项的未知数,然后再根据分母不等于0求解即可;
(2)根据加减消元的思想,消掉常数项的未知数,然后再根据分母等于0,则方程有无穷多解.
(2)根据加减消元的思想,消掉常数项的未知数,然后再根据分母等于0,则方程有无穷多解.
解答:(1)解:
,
②×2得,6x+2y=6③,
③-①得,(6-a)x=5,
当a≠6时,方程有唯一的解x=
;
(2)解:
①×2得,2x+4y=2③,
③-②得,(4-m)y=0,
当4-m=0,
即m=4,有无穷多解.
|
②×2得,6x+2y=6③,
③-①得,(6-a)x=5,
当a≠6时,方程有唯一的解x=
| 5 |
| 6-a |
(2)解:
|
①×2得,2x+4y=2③,
③-②得,(4-m)y=0,
当4-m=0,
即m=4,有无穷多解.
点评:本题考查了二元一次方程组的解的拓广,注意当未知数的系数不等于0时,有唯一解,当未知数的系数等于0时,方程有无穷多解或无解.

练习册系列答案
相关题目
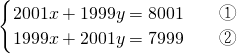
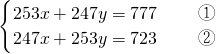 .
.