��Ŀ����
����Ŀ����ͼ��������y=ax2+bx+3��x���ཻ�ڵ�A����1��0����B��3��0������y���ཻ�ڵ�C����PΪ�߶�OB�ϵĶ��㣨����O��B�غϣ�������P��ֱ��x���ֱ�����������߶�BC�ֱ��ڵ�E��F����D��y���������ϣ�OD=2������DE��OF��
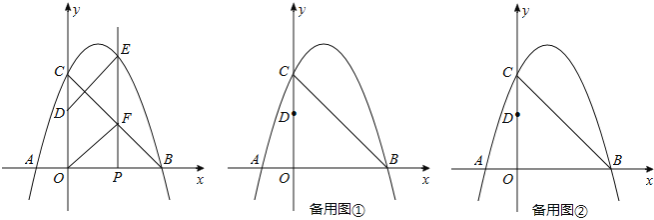
��1���������ߵĽ���ʽ��
��2�����ı���ODEF��ƽ���ı���ʱ�����P�����ꣻ
��3������A��ֱ�߽���2���е�ƽ���ı���ODEF�ֳ������ȵ������֣�������ֱ�ߵĽ���ʽ��������˵��ƽ��ƽ���ı�����������ɣ�
���𰸡���1��y=��x2+2x+3����2����1��0����2��0������3��y=![]() x+
x+![]() ��y=
��y=![]() x+
x+![]() ��
��
��������
�����������1�����ô���ϵ������������ߵĽ���ʽ��
��2��ƽ���ı��εĶԱ���ȣ����EF=OD=2���ݴ��з��������P�����ꣻ
��3�������������ĶԳƵ�������⣮ƽ���ı��������ĶԳ�ͼ�Σ���Գ�����Ϊ�����Խ��ߵĽ��㣨��Խ��ߵ��е㣩�����Գ����ĵ�ֱ��ƽ��ƽ���ı��ε��������˹���A��ODEF�Գ����ĵ�ֱ��ƽ��ODEF�������
�⣺��1������A����1��0����B��3��0����������y=ax2+bx+3�ϣ�
��![]() ��
��
���a=��1��b=2��
�������ߵĽ���ʽΪ��y=��x2+2x+3��
��2���������߽���ʽy=��x2+2x+3�У���x=0����y=3��
��C��0��3����
��ֱ��BC�Ľ���ʽΪy=kx+b����B��3��0����C��0��3���������ã�
![]() ��
��
���k=��1��b=3��
��y=��x+3��
��E��������x����x2+2x+3������P��x��0����F��x����x+3����
��EF=yE��yF=��x2+2x+3������x+3��=��x2+3x��
���ı���ODEF��ƽ���ı��Σ�
��EF=OD=2��
����x2+3x=2����x2��3x+2=0��
���x=1��x=2��
��P��������1��0����2��0����
��3��ƽ���ı��������ĶԳ�ͼ�Σ���Գ�����Ϊ�����Խ��ߵĽ��㣨��Խ��ߵ��е㣩�����Գ����ĵ�ֱ��ƽ��ƽ���ı��ε��������˹���A��ODEF�Գ����ĵ�ֱ��ƽ��ODEF�������
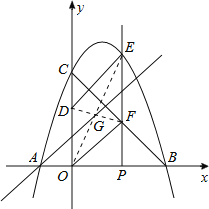
����P��1��0��ʱ��
��F������1��2������D��0��2����
��Խ���DF���е�ΪG����G��![]() ��2����
��2����
��ֱ��AG�Ľ���ʽΪy=kx+b����A����1��0����G��![]() ��2���������ã�
��2���������ã�
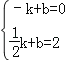 ��
��
���k=b=![]() ��
��
������ֱ�ߵĽ���ʽΪ��y=![]() x+
x+![]() ��
��
����P��
��F������2��1������D��0��2����
��Խ���DF���е�ΪG����G��1��![]() ����
����
��ֱ��AG�Ľ���ʽΪy=kx+b����A����1��0����G��1��![]() ���������ã�
���������ã�
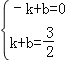 ��
��
���k=b=![]() ��
��
������ֱ�ߵĽ���ʽΪ��y=![]() x+
x+![]() ��
��
��������������ֱ�ߵĽ���ʽΪ��y=![]() x+
x+![]() ��y=
��y=![]() x+
x+![]() ��
��