题目内容
【题目】解答
(1)如图1,小明和小亮在研究一个数学问题:已知AB∥CD,AB和CD都不经过点P,探索∠P与∠A,∠C的数量关系. 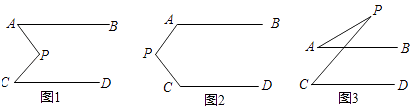
小明是这样证明的:过点P作PQ∥AB
∴∠APQ=∠A()
∵PQ∥AB,AB∥CD.
∴PQ∥CD()
∴∠CPQ=∠C
∴∠APQ+∠CPQ=∠A+∠C
即∠APC=∠A+∠C
小亮是这样证明的:过点作PQ∥AB∥CD.
∴∠APQ=∠A,∠CPQ=∠C
∴∠APQ+∠CPQ=∠A+∠C
即∠APC=∠A+∠C
请在上面证明过程的过程的横线上,填写依据;两人的证明过程中,完全正确的是 .
(2)应用:
在图2中,若∠A=120°,∠C=140°,则∠APC的度数为;
(3)拓展:
在图3中,探索∠APC与∠A,∠C的数量关系,并说明理由.
【答案】
(1)两直线平行,内错角相等;平行于同一条直线的两条直线互相平行;小明
(2)100°
(3)解:∠APC=∠C﹣∠A,
理由是:如图3,∵AB∥CD,
∴∠C=∠POB,
∵∠APC=∠POB﹣∠A,
∴∠APC=∠C﹣∠A
【解析】解:(1)如图1,过点P作PQ∥AB, 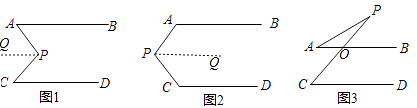
∴∠APQ=∠A(两直线平行,内错角相等),
∵PQ∥AB,AB∥CD,
∴PQ∥CD(平行于同一直线的两直线平行),
∴∠CPQ=∠C,
∴∠APQ+∠CPQ=∠A+∠C,
即∠APC=∠A+∠C;
所以答案是:两直线平行,内错角相等,平行于同一条直线的两条直线互相平行,小明;
2)如图2,过P作PQ∥AB,
∵AB∥CD,
∴PQ∥AB∥CD,
∴∠A+∠APQ=180°,∠C+∠CPQ=180°,
∵∠A=120°,∠C=140°,
∴∠APQ=60°,∠CPQ=40°,
∴∠APC=∠APQ+∠CPQ=100°,
所以答案是:100°;
【考点精析】掌握平行线的判定与性质是解答本题的根本,需要知道由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质.

 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案