题目内容
如图,在航线L的两侧分别有观测点A和B,点A到航线L的距离为2km,点B位于点A北偏东60°方向且与A相距5km处.现有一艘轮船正沿该航线自西向东航行,在C点观测到点A位于南偏东54°方向,航行10分钟后,在D点观测到点B位于北偏东70°方向.(1)求观测点B到航线L的距离;
(2)求该轮船航线的速度(结果精确到0.1km/h,参考数据:
| 3 |
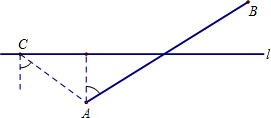
分析:(1)BF=BG-FG,在直角三角形ABG中,利用三角函数求得BG即可;
(2)根据CD=CM+AG-DF,利用三角函数求得CM,DF即可求解.
(2)根据CD=CM+AG-DF,利用三角函数求得CM,DF即可求解.
解答: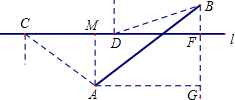 解:(1)BF=BG-FG,
解:(1)BF=BG-FG,
=ABsin30°-FG,
=5×0.5-2=0.5km;
(2)∵AG=ABcos30°=5×
=4.325,
∵DF=BFtan70°=0.5×2.75=1.375<AG,
∴点D在M的右侧,
∵CM=AMtan54°=2×1.38=2.76,
∴CD=CM+AG-DF,
=2.76+4.325-1.375,
=5.71.
所以轮船的速度是5.71÷10×60=34.26km/h≈34.3km/h.
 解:(1)BF=BG-FG,
解:(1)BF=BG-FG,=ABsin30°-FG,
=5×0.5-2=0.5km;
(2)∵AG=ABcos30°=5×
| ||
| 2 |
∵DF=BFtan70°=0.5×2.75=1.375<AG,
∴点D在M的右侧,
∵CM=AMtan54°=2×1.38=2.76,
∴CD=CM+AG-DF,
=2.76+4.325-1.375,
=5.71.
所以轮船的速度是5.71÷10×60=34.26km/h≈34.3km/h.
点评:本题主要考查了方向角的有关计算,正确记忆三角函数的定义是解决本题的关键.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
 ≈1.73,sin76°≈0.97,cos76°≈0.24,tan76°≈4.01)
≈1.73,sin76°≈0.97,cos76°≈0.24,tan76°≈4.01)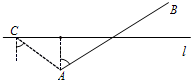 于南偏东54°方向,航行10分钟后,在D点观测到点B位于北偏东70°方向.
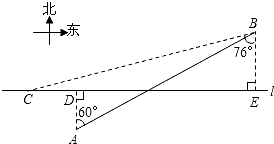
于南偏东54°方向,航行10分钟后,在D点观测到点B位于北偏东70°方向.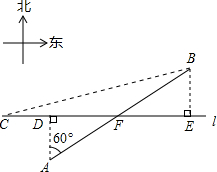 (2013•崇明县一模)如图,在航线l的两侧分别有观测点A和B,点A到航线l的距离为2海里,点B位于点A北偏东60°方向且与A相距l0海里处.现有一艘轮船从位于点B南偏西76°方向的C处,正沿该航线自西向东航行,10分钟后该轮船行至点A的正北方向的D处.
(2013•崇明县一模)如图,在航线l的两侧分别有观测点A和B,点A到航线l的距离为2海里,点B位于点A北偏东60°方向且与A相距l0海里处.现有一艘轮船从位于点B南偏西76°方向的C处,正沿该航线自西向东航行,10分钟后该轮船行至点A的正北方向的D处.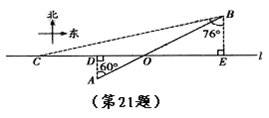
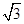 =1.73,sin76°=0.97,cos76°=0.4,tan76°=4.01)
=1.73,sin76°=0.97,cos76°=0.4,tan76°=4.01)