题目内容
抛物线y=x2+2x+3与x轴的交点的个数有
- A.0个
- B.1个
- C.2个
- D.3个
A
分析：根据b2-4ac与零的关系即可判断出二次函数y=x2+2x+3的图象与x轴交点的个数．
解答：∵b2-4ac=4-4×1×3=-8＜0
∴二次函数y=x2+2x+3的图象与x轴没有交点．
故选A
点评：考查二次函数y=ax2+bx+c的图象与x轴交点的个数的判断．
分析：根据b2-4ac与零的关系即可判断出二次函数y=x2+2x+3的图象与x轴交点的个数．
解答：∵b2-4ac=4-4×1×3=-8＜0
∴二次函数y=x2+2x+3的图象与x轴没有交点．
故选A
点评：考查二次函数y=ax2+bx+c的图象与x轴交点的个数的判断．
练习册系列答案
相关题目
抛物线y=x2+2x-2的图象上最低点的坐标是（ ）
| A、（2，-2） | B、（1，-2） | C、（1，-3） | D、（-1，-3） |
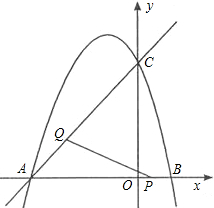秒，请求出△APQ的面积S与t的函数关系式，并求出当t为何值时，△APQ的面积最大，最大面积是多少？