Question

若抛物线y=x²+2x-1上有两点A、B，且原点位于线段AB的三等分点处，则这两点的坐标为

 

．

Answer 1

分析：过A作AE⊥x轴于E，过B作BF⊥x轴于F，分两种情况：
（1）当OA=2OB时，设B（a，b），（a＞0，b＞0）则A的坐标是（-2a，-2b），代入y=x²+2x-1即可求出A、B的坐标；
（2）当2OA=OB时，与（1）方法类似即可求出A、B的坐标．

解答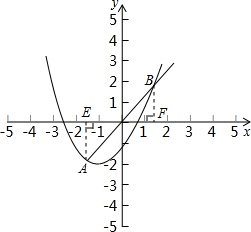：解：过A作AE⊥x轴于E，过B作BF⊥x轴于F，
（1）当OA=2OB时，如图
设B（a，b），（a＞0，b＞0）则A的坐标是（-2a，-2b），代入y=x²+2x-1得：

b=a2+2a-1 -2b=4a2-4a-1

，
解得：a=

6

6

，b=

6

3

-

5

6

，
∴-2a=-

6

3

，-2b=-

2 6

3

-

5

3

，
∴A（-

6

3

，-

2 6

3

-

5

3

），B（

6

6

，

6

3

-

5

6

）；

（2）当2OA=OB时，与（1）解法类似可求出A（-

6

6

，-

6

6

-

5

6

），B（

6

3

，

6

3

+

5

3

）．
故答案为：（-

6

3

，-

2 6

3

-

5

3

），（

6

6

，

6

3

-

5

6

）或（-

6

6

，-

6

6

-

5

6

），（

6

3

，

6

3

+

5

3

）．

点评：本题主要考查了二次函数图象上点的特征，平行线分线段成比例定理，解二元二次方程组等知识点，解此题的关键是设出A和B的坐标，代入解析式能求出方程的解．