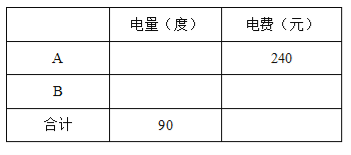
题目内容
【题目】如图,四边形ABCD是边长为a的正方形,点G,E分别是边AB,BC的中点,∠AEF=90°,且EF交正方形外角的平分线CF于点F.
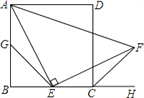
(1)证明:△AGE≌△ECF;
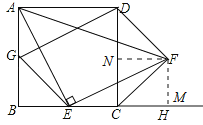
(2)连接GD,DF.判断四边形GEFD的形状,并说明理由;
【答案】(1)详见解析; (2)平行四边形
【解析】(1)证明:∵正方形ABCD,点G,E为边AB、BC中点,∴AG=EC,△BEG为等腰直角三角形,∴∠AGE=180°﹣45°=135°,又∵CF为正方形外角平分线,∴∠ECF=90°+45°=135°,∵∠AEF=90°,∴∠GAE=90°﹣∠AEB=∠CEF,在△AGE和△ECF中,∵∠AGE=∠ECF,AG=CE,∠GAE=∠CEF,∴△AGE≌△ECF(ASA);
(2)四边形GEFD是平行四边形,理由如下:过点F作FM⊥BH于M,过F作FN⊥DC于N,易证△AGD≌△ABE,∴GD=AE,∠BAE=∠ADG,∵△AGE≌△ECF,∴AE=EF,∴GD=EF,在△AGD和△EFM中,∵∠DAG=∠FHE=90°,∠ADG=∠FEH,GD=FE,∴△AGD≌△EFM(AAS),∴GD=EF,在△DFN和△BGE中,∵DN=BE,∠DNF=∠B=90°,NF=BG,∴△DFN≌△BGE( SAS),∴DF=GE,∴四边形GEFD是平行四边形.

练习册系列答案
相关题目