题目内容
已知A(1,5),B(3,-1)两点,在x轴上取一点M,使AM-BN取得最大值时,则M的坐标为 ▲
(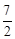 ,0)。
,0)。
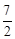 ,0)。
,0)。一次函数综合题,线段中垂线的性质,三角形三边关系,关于x轴对称的点的坐标,待定系数法,直线上点的坐标与方程的关系,解二元一次方程组。
【分析】如图,作点B关于x轴的对称点B′,连接AB′并延长与x轴的交点,即为所求的M点。
此时AM-BM=AM-B′M=AB′。
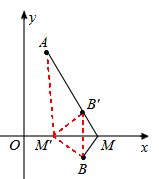
不妨在x轴上任取一个另一点M′,连接M′A、M′B、M′B.
则M′A-M′B=M′A-M′B′<AB′(三角形两边之差小于第三边)。
∴M′A-M′B<AM-BM,即此时AM-BM最大。
∵B′是B(3,-1)关于x轴的对称点,∴B′(3,1)。
设直线AB′解析式为y=kx+b,把A(1,5)和B′(3,1)代入得:
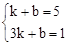 ,解得
,解得 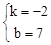 。∴直线AB′解析式为y=-2x+7。
。∴直线AB′解析式为y=-2x+7。
令y=0,解得x=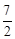 。∴M点坐标为(
。∴M点坐标为(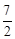 ,0)。
,0)。
【分析】如图,作点B关于x轴的对称点B′,连接AB′并延长与x轴的交点,即为所求的M点。
此时AM-BM=AM-B′M=AB′。

不妨在x轴上任取一个另一点M′,连接M′A、M′B、M′B.
则M′A-M′B=M′A-M′B′<AB′(三角形两边之差小于第三边)。
∴M′A-M′B<AM-BM,即此时AM-BM最大。
∵B′是B(3,-1)关于x轴的对称点,∴B′(3,1)。
设直线AB′解析式为y=kx+b,把A(1,5)和B′(3,1)代入得:
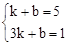 ,解得
,解得 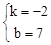 。∴直线AB′解析式为y=-2x+7。
。∴直线AB′解析式为y=-2x+7。令y=0,解得x=
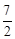 。∴M点坐标为(
。∴M点坐标为(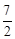 ,0)。
,0)。
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目





 为
为 ,运动时间为
,运动时间为 ,则下列图形能大致地刻画
,则下列图形能大致地刻画
 (年)逐年成直线上升,y与
(年)逐年成直线上升,y与
 、
、 两地相距10千米,甲班从
两地相距10千米,甲班从 小时,甲、乙两班离
小时,甲、乙两班离 千米、
千米、 千米,
千米,
 (
( )的图象不经过
)的图象不经过