题目内容
如图所示的图案是有边长相等的黑白两色正方形按照一定规律拼接而成.
(1)观察图形,填写下表:
(2)推测第6个图形中,黑色正方形的个数是
(3)推测第n个图形中,黑色正方形的个数是

(1)观察图形,填写下表:
| 图序 | 1 | 2 | 3 | … |
| 黑色正方形个数 | 1 1 |
2 2 |
3 3 |
4 4 |
| 白色正方形个数 | 8 8 |
13 13 |
18 18 |
23 23 |
6
6
,白色正方形的个数是33
33
.(3)推测第n个图形中,黑色正方形的个数是
n
n
,白色正方形的个数是5n+3
5n+3
(都用含n的代数式表示)分析:(1)根据图形直接数出结果即可;
(2)黑色正方形的个数等同于图形的个数,后一个图形比前一个图形多5个白色正方形,据此规律解答;
(3)利用以上两题的分析结果可以得到则第n个图形白色正方形的个数为5n+3;
(2)黑色正方形的个数等同于图形的个数,后一个图形比前一个图形多5个白色正方形,据此规律解答;
(3)利用以上两题的分析结果可以得到则第n个图形白色正方形的个数为5n+3;
解答:解:(1)填表如下:
(2)推测第6个图形中,黑色正方形的个数是 6,白色正方形的个数是 33.
(3)推测第n个图形中,黑色正方形的个数是 n,白色正方形的个数是 5n+3;
故
| 图序 | 1 | 2 | 3 | … |
| 黑色正方形个数 | 1 | 2 | 3 | 4 |
| 白色正方形个数 | 8 | 13 | 18 | 23 |
(3)推测第n个图形中,黑色正方形的个数是 n,白色正方形的个数是 5n+3;
故
点评:本题主要考查了图形的一般规律性变化问题,能够通过观察掌握其内在规律,进而求解.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
某数学研究所门前有一个边长为4米的正方形花坛,花坛内部要用红、黄、紫三种颜色的花草种植成如图所示的图案,图案中AE=MN.准备在形如Rt△MEH的四个全等三角形内种植黄色花草,在形如Rt△AEH的四个全等三角形内种植红色花草,在正方形MNPQ内种植紫色花草,每种花草的价格如下表:
设AE的长为x米,正方形EFGH的面积为S平方米,买花草所需的费用为W元,解答下列问题:
(1)S与x之间的函数关系式为S= ;
(2)求W与x之间的函数关系式,并求所需的最低费用是多少元;
(3)当买花草所需的费用最低时,求EM的长.
| 品 种 | 红色花草 | 黄色花草 | 紫色花草 |
| 价格(元/米2) | 60 | 80 | 120 |

(1)S与x之间的函数关系式为S=
(2)求W与x之间的函数关系式,并求所需的最低费用是多少元;
(3)当买花草所需的费用最低时,求EM的长.
某数学研究所门前有一个边长为4米的正方形花坛,花坛内部要用红、黄、紫三种颜色的花草种植成如图所示的图案,图案中 .准备在形如Rt
.准备在形如Rt 的四个全等三角形内种植红色花草,在形如Rt△EMH的四个全等三角形内种植黄色花草,在正方形
的四个全等三角形内种植红色花草,在形如Rt△EMH的四个全等三角形内种植黄色花草,在正方形 内种植紫色花草,每种花草的价格如下表:
内种植紫色花草,每种花草的价格如下表:
设 的长为
的长为 米,正方形
米,正方形 的面积为
的面积为 平方米,买花草所需的费用为
平方米,买花草所需的费用为 元,解答下列问题:
元,解答下列问题:
(1) 与
与 之间的函数关系式为
之间的函数关系式为 ;
;
(2)求 与
与 之间的函数关系式,并求所需的最低费用是多少元;
之间的函数关系式,并求所需的最低费用是多少元;
(3)当买花草所需的费用最低时,求 的长.
的长.

 .准备在形如Rt
.准备在形如Rt 的四个全等三角形内种植红色花草,在形如Rt△EMH的四个全等三角形内种植黄色花草,在正方形
的四个全等三角形内种植红色花草,在形如Rt△EMH的四个全等三角形内种植黄色花草,在正方形 内种植紫色花草,每种花草的价格如下表:
内种植紫色花草,每种花草的价格如下表:| 品种 | 红色花草 | 黄色花草 | 紫色花草 |
| 价格(元/米2) | 60 | 80 | 120 |
 的长为
的长为 米,正方形
米,正方形 的面积为
的面积为 平方米,买花草所需的费用为
平方米,买花草所需的费用为 元,解答下列问题:
元,解答下列问题:(1)
 与
与 之间的函数关系式为
之间的函数关系式为 ;
;(2)求
 与
与 之间的函数关系式,并求所需的最低费用是多少元;
之间的函数关系式,并求所需的最低费用是多少元;(3)当买花草所需的费用最低时,求
 的长.
的长.
某数学研究所门前有一个边长为4米的正方形花坛,花坛内部要用红、黄、紫三种颜色的花草种植成如图所示的图案,图案中 .准备在形如Rt
.准备在形如Rt 的四个全等三角形内种植红色花草,在形如Rt△EMH的四个全等三角形内种植黄色花草,在正方形
的四个全等三角形内种植红色花草,在形如Rt△EMH的四个全等三角形内种植黄色花草,在正方形 内种植紫色花草,每种花草的价格如下表:
内种植紫色花草,每种花草的价格如下表:
|
品种 |
红色花草 |
黄色花草 |
紫色花草 |
|
价格(元/米2) |
60 |
80 |
120 |
设 的长为
的长为 米,正方形
米,正方形 的面积为
的面积为 平方米,买花草所需的费用为
平方米,买花草所需的费用为 元,解答下列问题:
元,解答下列问题:
(1) 与
与 之间的函数关系式为
之间的函数关系式为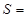 ;
;
(2)求 与
与 之间的函数关系式,并求所需的最低费用是多少元;
之间的函数关系式,并求所需的最低费用是多少元;
(3)当买花草所需的费用最低时,求 的长.
的长.

