题目内容
某数学研究所门前有一个边长为4米的正方形花坛,花坛内部要用红、黄、紫三种颜色的花草种植成如图所示的图案,图案中AE=MN.准备在形如Rt△MEH的四个全等三角形内种植黄色花草,在形如Rt△AEH的四个全等三角形内种植红色花草,在正方形MNPQ内种植紫色花草,每种花草的价格如下表:| 品 种 | 红色花草 | 黄色花草 | 紫色花草 |
| 价格(元/米2) | 60 | 80 | 120 |

(1)S与x之间的函数关系式为S=
(2)求W与x之间的函数关系式,并求所需的最低费用是多少元;
(3)当买花草所需的费用最低时,求EM的长.
分析:(1)依题意可知S=EH2,又EH2=AE2+AH2,代入数据可得S=x2+(4-x)2
(2)由二次函数的性质,通过配方的方法求得最大值
(3)根据相关关系列出方程,解方程即可得出答案
(2)由二次函数的性质,通过配方的方法求得最大值
(3)根据相关关系列出方程,解方程即可得出答案
解答:解:(1)由分析(1)可得答案
S=x2+(4-x)2或2x2-8x+16.(2分)
(2)W=60×4S△AEH+80(S正方形EFGH-S正方形MNPQ)+120S正方形MNPQ
=60×4×
x(4-x)+80[x2+(4-x)2-x2]+120x2(4分)
=80x2-160x+1280.(5分)
配方得W=80(x-1)2+1200.(6分)
∴当x=1时,W最小值=1200元.(7分)
(3)因为四个黄颜色的直角三角形全等,所以EM=QH,
设EM=a米,则MH=MQ+QH=MQ+EM=(a+1)米.
在Rt△EMH中,a2+(a+1)2=12+32,
解得a=
∵a>0
∴a=
∴EM的长为
米.(10分)
S=x2+(4-x)2或2x2-8x+16.(2分)
(2)W=60×4S△AEH+80(S正方形EFGH-S正方形MNPQ)+120S正方形MNPQ
=60×4×
| 1 |
| 2 |
=80x2-160x+1280.(5分)
配方得W=80(x-1)2+1200.(6分)
∴当x=1时,W最小值=1200元.(7分)
(3)因为四个黄颜色的直角三角形全等,所以EM=QH,
设EM=a米,则MH=MQ+QH=MQ+EM=(a+1)米.
在Rt△EMH中,a2+(a+1)2=12+32,
解得a=
-1±
| ||
| 2 |
∴a=
| ||
| 2 |
∴EM的长为
| ||
| 2 |
点评:求二次函数的最大(小)值有三种方法,第一种可由图象直接得出,第二种是配方法,第三种是公式法,常用的是后两种方法,当二次系数a的绝对值是较小的整数时,用配方法较好,如y=-x2-2x+5,y=3x2-6x+1等用配方法求解比较简单.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
某数学研究所门前有一个边长为4米的正方形花坛,花坛内部要用红、黄、紫三种颜色的花草种植成如图所示的图案,图案中![]() .准备在形如Rt
.准备在形如Rt![]() 的四个全等三角形内种植红色花草,在形如Rt△EMH的四个全等三角形内种植黄色花草,在正方形
的四个全等三角形内种植红色花草,在形如Rt△EMH的四个全等三角形内种植黄色花草,在正方形![]() 内种植紫色花草,每种花草的价格如下表:
内种植紫色花草,每种花草的价格如下表:
| 品种 | 红色花草 | 黄色花草 | 紫色花草 |
| 价格(元/米2) | 60 | 80 | 120 |
设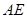 的长为
的长为![]() 米,正方形
米,正方形![]() 的面积为
的面积为![]() 平方米,买花草所需的费用为
平方米,买花草所需的费用为![]() 元,解答下列问题:
元,解答下列问题:
(1)![]() 与
与![]() 之间的函数关系式为
之间的函数关系式为![]() ;
;
(2)求![]() 与
与![]() 之间的函数关系式,并求所需的最低费用是多少元;
之间的函数关系式,并求所需的最低费用是多少元;
(3)当买花草所需的费用最低时,求![]() 的长.
的长.

某数学研究所门前有一个边长为4米的正方形花坛,花坛内部要用红、黄、紫三种颜色的花草种植成如图所示的图案,图案中 .准备在形如Rt
.准备在形如Rt 的四个全等三角形内种植红色花草,在形如Rt△EMH的四个全等三角形内种植黄色花草,在正方形
的四个全等三角形内种植红色花草,在形如Rt△EMH的四个全等三角形内种植黄色花草,在正方形 内种植紫色花草,每种花草的价格如下表:
内种植紫色花草,每种花草的价格如下表:
设 的长为
的长为 米,正方形
米,正方形 的面积为
的面积为 平方米,买花草所需的费用为
平方米,买花草所需的费用为 元,解答下列问题:
元,解答下列问题:
(1) 与
与 之间的函数关系式为
之间的函数关系式为 ;
;
(2)求 与
与 之间的函数关系式,并求所需的最低费用是多少元;
之间的函数关系式,并求所需的最低费用是多少元;
(3)当买花草所需的费用最低时,求 的长.
的长.

 .准备在形如Rt
.准备在形如Rt 的四个全等三角形内种植红色花草,在形如Rt△EMH的四个全等三角形内种植黄色花草,在正方形
的四个全等三角形内种植红色花草,在形如Rt△EMH的四个全等三角形内种植黄色花草,在正方形 内种植紫色花草,每种花草的价格如下表:
内种植紫色花草,每种花草的价格如下表:| 品种 | 红色花草 | 黄色花草 | 紫色花草 |
| 价格(元/米2) | 60 | 80 | 120 |
 的长为
的长为 米,正方形
米,正方形 的面积为
的面积为 平方米,买花草所需的费用为
平方米,买花草所需的费用为 元,解答下列问题:
元,解答下列问题:(1)
 与
与 之间的函数关系式为
之间的函数关系式为 ;
;(2)求
 与
与 之间的函数关系式,并求所需的最低费用是多少元;
之间的函数关系式,并求所需的最低费用是多少元;(3)当买花草所需的费用最低时,求
 的长.
的长.
某数学研究所门前有一个边长为4米的正方形花坛,花坛内部要用红、黄、紫三种颜色的花草种植成如图所示的图案,图案中 .准备在形如Rt
.准备在形如Rt 的四个全等三角形内种植红色花草,在形如Rt△EMH的四个全等三角形内种植黄色花草,在正方形
的四个全等三角形内种植红色花草,在形如Rt△EMH的四个全等三角形内种植黄色花草,在正方形 内种植紫色花草,每种花草的价格如下表:
内种植紫色花草,每种花草的价格如下表:
| 品种 | 红色花草 | 黄色花草 | 紫色花草 |
| 价格(元/米2) | 60 | 80 | 120 |
 的长为
的长为 米,正方形
米,正方形 的面积为
的面积为 平方米,买花草所需的费用为
平方米,买花草所需的费用为 元,解答下列问题:
元,解答下列问题:(1)
 与
与 之间的函数关系式为
之间的函数关系式为 ;
;(2)求
 与
与 之间的函数关系式,并求所需的最低费用是多少元;
之间的函数关系式,并求所需的最低费用是多少元;(3)当买花草所需的费用最低时,求
 的长.
的长.
某数学研究所门前有一个边长为4米的正方形花坛,花坛内部要用红、黄、紫三种颜色的花草种植成如图所示的图案,图案中 .准备在形如Rt
.准备在形如Rt 的四个全等三角形内种植红色花草,在形如Rt△EMH的四个全等三角形内种植黄色花草,在正方形
的四个全等三角形内种植红色花草,在形如Rt△EMH的四个全等三角形内种植黄色花草,在正方形 内种植紫色花草,每种花草的价格如下表:
内种植紫色花草,每种花草的价格如下表:
|
品种 |
红色花草 |
黄色花草 |
紫色花草 |
|
价格(元/米2) |
60 |
80 |
120 |
设 的长为
的长为 米,正方形
米,正方形 的面积为
的面积为 平方米,买花草所需的费用为
平方米,买花草所需的费用为 元,解答下列问题:
元,解答下列问题:
(1) 与
与 之间的函数关系式为
之间的函数关系式为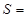 ;
;
(2)求 与
与 之间的函数关系式,并求所需的最低费用是多少元;
之间的函数关系式,并求所需的最低费用是多少元;
(3)当买花草所需的费用最低时,求 的长.
的长.
