题目内容
 如图,直角三角形ABC有一外接圆,其中∠B=90°,AB>BC,今欲在
如图,直角三角形ABC有一外接圆,其中∠B=90°,AB>BC,今欲在 上找一点P,使得
上找一点P,使得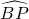 =
= ,以下是甲、乙两人的作法:
,以下是甲、乙两人的作法:
甲:(1)取AB中点D
(2)过D作直线AC的并行线,交 于P,则P即为所求
于P,则P即为所求
乙:(1)取AC中点E
(2)过E作直线AB的并行线,交 于P,则P即为所求
于P,则P即为所求
对于甲、乙两人的作法,下列判断何者正确?
- A.两人皆正确
- B.两人皆错误
- C.甲正确,乙错误C
- D.甲错误,乙正确
D
分析:(1)由甲的作法可知,DP是△ABC的中位线,由于DP不垂直于BC,故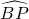 ≠
≠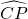 ;
;
(2)由乙的作法,连BE,可知△BEC为等腰三角形,由等腰三角形的性质可知∠1=∠2,根据圆周角定理即可得出结论.
解答: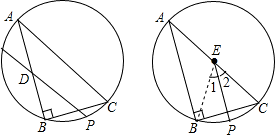 解:(1)由甲的作法可知,DP是△ABC的中位线,
解:(1)由甲的作法可知,DP是△ABC的中位线,
∵DP不垂直于BC,
∴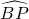 ≠
≠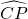 ;
;
(2)由乙的作法,连BE,可知△BEC为等腰三角形
∵直线PE⊥BC,
∴∠1=∠2
故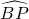 =
=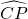 ;
;
∴甲错误,乙正确.
故选D.
点评:本题考查的是垂径定理、三角形的中位线定理及圆周角定理,熟知同弧或等弧所对的圆周角相等是解答此题的关键.
分析:(1)由甲的作法可知,DP是△ABC的中位线,由于DP不垂直于BC,故
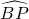 ≠
≠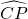 ;
;(2)由乙的作法,连BE,可知△BEC为等腰三角形,由等腰三角形的性质可知∠1=∠2,根据圆周角定理即可得出结论.
解答:
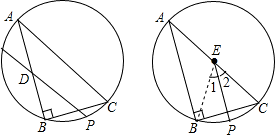 解:(1)由甲的作法可知,DP是△ABC的中位线,
解:(1)由甲的作法可知,DP是△ABC的中位线,∵DP不垂直于BC,
∴
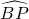 ≠
≠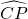 ;
;(2)由乙的作法,连BE,可知△BEC为等腰三角形
∵直线PE⊥BC,
∴∠1=∠2
故
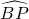 =
=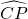 ;
;∴甲错误,乙正确.
故选D.
点评:本题考查的是垂径定理、三角形的中位线定理及圆周角定理,熟知同弧或等弧所对的圆周角相等是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
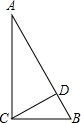 如图,直角三角形ABC中∠ACB=90°,CD是高,∠A=30°,AB=4.则BD=
如图,直角三角形ABC中∠ACB=90°,CD是高,∠A=30°,AB=4.则BD= 如图,直角三角形ABC的直角边AB=6,以AB为直径画半圆,若阴影部分的面积S1-S2=
如图,直角三角形ABC的直角边AB=6,以AB为直径画半圆,若阴影部分的面积S1-S2=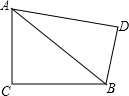 如图在直角三角形ABC的斜边AB上另作直角三角形ABD,并以AB为斜边,若BC=1,AC=m,AD=2,则BD等于( )
如图在直角三角形ABC的斜边AB上另作直角三角形ABD,并以AB为斜边,若BC=1,AC=m,AD=2,则BD等于( ) 如图,直角三角形ACB中,CD是斜边AB上的中线,若AC=8cm,BC=6cm,那么△ACD与△BCD的周长差为
如图,直角三角形ACB中,CD是斜边AB上的中线,若AC=8cm,BC=6cm,那么△ACD与△BCD的周长差为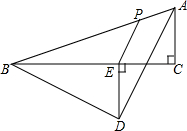 如图,直角三角形ABC中,∠C=90°,P,E分别是边AB,BC上的点,D为△ABC外一点,DE⊥BC,DE=EC,BE=2EC,∠BDE=∠PEC,AD∥PE,AC=4,则线段BC的长为
如图,直角三角形ABC中,∠C=90°,P,E分别是边AB,BC上的点,D为△ABC外一点,DE⊥BC,DE=EC,BE=2EC,∠BDE=∠PEC,AD∥PE,AC=4,则线段BC的长为