题目内容
【题目】如图，在矩形ABCD中，对角线AC的垂直平分线EF分别交AD、AC、BC于点E、O、F，连接CE和AF.
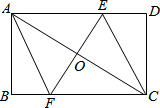
（1）求证：四边形AECF为菱形；
（2）若AB＝4，BC＝8，求菱形AECF的周长.
【答案】（1）见解析；（2）20
【解析】
（1）根据ASA推出：△AEO≌△CFO；根据全等得出OE=OF，推出四边形是平行四边形，再根据EF⊥AC即可推出四边形是菱形；
（2）根据线段垂直平分线性质得出AF=CF，设AF=x，推出AF=CF=x，BF=8－x．在Rt△ABF中，由勾股定理求出x的值，即可得到结论．
（1）∵EF是AC的垂直平分线，∴AO=OC，∠AOE=∠COF=90°．
∵四边形ABCD是矩形，∴AD∥BC，∴∠EAO=∠FCO．
在△AEO和△CFO中，∵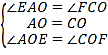
，∴△AEO≌△CFO（ASA）；∴OE=OF．
又∵OA=OC，∴四边形AECF是平行四边形．
又∵EF⊥AC，∴平行四边形AECF是菱形；
（2）设AF=x．
∵EF是AC的垂直平分线，∴AF=CF=x，BF=8﹣x．在Rt△ABF中，由勾股定理得：AB2+BF2=AF2，∴42+（8﹣x）2=x2，解得：x=5，∴AF=5，∴菱形AECF的周长为20．
练习册系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
