题目内容
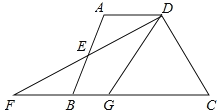
【题目】如图,在四边形![]() 中,
中, ![]() ,
,![]() 是
是![]() 的中点,连接
的中点,连接![]() 并延长交
并延长交![]() 的延长线于点
的延长线于点![]() ,点
,点![]() 在边
在边![]() 上,且
上,且![]() .
.
(1)求证:![]() ≌
≌![]() .
.
(2)连接![]() ,判断
,判断![]() 与
与![]() 的位置关系并说明理由.
的位置关系并说明理由.
【答案】(1)见解析;(2)![]() ,见解析
,见解析
【解析】
(1)由AD与BC平行,利用两直线平行内错角相等,得到一对角相等,再由一对对顶角相等及E为AB中点得到一对边相等,利用AAS即可得出△ADE≌△BFE;
(2)∠GDF=∠ADE,以及(1)得出的∠ADE=∠BFE,等量代换得到∠GDF=∠BFE,利用等角对等边得到GF=GD,即三角形GDF为等腰三角形,再由(1)得到DE=FE,即GE为底边上的中线,利用三线合一即可得到GE与DF垂直.
(1)证明:∵AD∥BC,
∴∠ADE=∠BFE,
∵E为AB的中点,
∴AE=BE,
在△ADE和△BFE中,
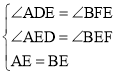 ,
,
∴△ADE≌△BFE(AAS);
(2)EG⊥DF,
理由如下:连接EG,
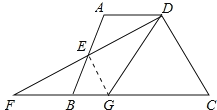
∵∠GDF=∠ADE,∠ADE=∠BFE,
∴∠GDF=∠BFE,
∴DG=FG,
由(1)得:△ADE≌△BFE
∴DE=FE,
即GE为DF上的中线,
又∵DG=FG,
∴EG⊥DF.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目