题目内容
29、已知四边形ABCD的对角线AC、BD相交于点O,给出下列5个条件:
①AD∥BC;②AB∥CD;③∠ABC=∠ADC;④AB=CD;⑤OB=OD;
(1)从以上5个条件中任意选取2个条件,能推出四边形ABCD是平行四边形的,除“①与②”外,还有哪几种?(请用序号表示)
(2)除“①与②”外,选择你写的其中的一种,画出示意图,写出已知,求证和证明.
①AD∥BC;②AB∥CD;③∠ABC=∠ADC;④AB=CD;⑤OB=OD;
(1)从以上5个条件中任意选取2个条件,能推出四边形ABCD是平行四边形的,除“①与②”外,还有哪几种?(请用序号表示)
(2)除“①与②”外,选择你写的其中的一种,画出示意图,写出已知,求证和证明.
分析:(1)根据平行四边形的5种判定方法,能推出四边形ABCD是平行四边形的有①③,②③,②④,①⑤,②⑤;
(2)可选②③加以证明.
(2)可选②③加以证明.
解答:解:(1)还有①与③,②与③,②与④,①与⑤,②与⑤;
(2)已知:如图,在四边形ABCD中,AB∥CD,∠ABC=∠ADC,

求证:四边形ABCD是平行四边形.
证明:∵AB∥CD,
∴∠ABC+∠BCD=180°
又∵∠ABC=∠ADC,
∴∠BCD+∠ADC=180°
∴BC∥AD.
∴四边形ABCD是平行四边形.
(2)已知:如图,在四边形ABCD中,AB∥CD,∠ABC=∠ADC,

求证:四边形ABCD是平行四边形.
证明:∵AB∥CD,
∴∠ABC+∠BCD=180°
又∵∠ABC=∠ADC,
∴∠BCD+∠ADC=180°
∴BC∥AD.
∴四边形ABCD是平行四边形.
点评:本题考查了平行四边形的判定,熟练掌握判定定理是解题的关键.

练习册系列答案
 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
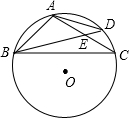 如图,已知四边形ABCD的外接圆⊙O的半径为2,对角线AC与BD的交点为E,AE=EC,AB=
如图,已知四边形ABCD的外接圆⊙O的半径为2,对角线AC与BD的交点为E,AE=EC,AB=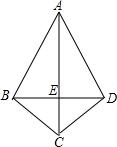 如图,△ABC与△ADC关于直线AC对称,连接BD,若已知四边形ABCD的面积是125,AC=25,则BD的长为
如图,△ABC与△ADC关于直线AC对称,连接BD,若已知四边形ABCD的面积是125,AC=25,则BD的长为 如图,已知四边形ABCD的对角线互相垂直,若适当添加一个条件,就能判定该四边形是菱形.那么这个条件可以是( )
如图,已知四边形ABCD的对角线互相垂直,若适当添加一个条件,就能判定该四边形是菱形.那么这个条件可以是( ) 如图,已知四边形ABCD的四个顶点的坐标分别为A(0,0),B(9,0),C(7,5),D(2,7),将该四边形各顶点的横坐标都增加2,纵坐标都增加3,其面积为( )
如图,已知四边形ABCD的四个顶点的坐标分别为A(0,0),B(9,0),C(7,5),D(2,7),将该四边形各顶点的横坐标都增加2,纵坐标都增加3,其面积为( )