Question

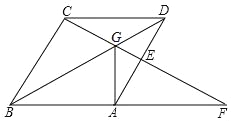
【题目】已知菱形ABCD中，AB=8，点G是对角线BD上一点，CG交BA的延长线于点F．

（1）求证：CG2=GEGF；

（2）如果DG=GB，且AG⊥BF，求cos∠F．

Answer 1

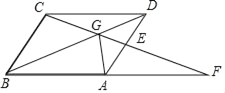
【答案】（1）证明见解析；（2）；

【解析】

（1）利用菱形的性质易证△ADG≌△CDG，由全等三角形的性质可得：∠DAG=∠DCG，再根据菱形的性质可得∠F=∠DCG=∠DAG，所以△GAE∽△GFA，由相似三角形的性质即可证明CG2=GEGF；
（2）易证△DAG∽△DBA，由相似三角形的性质可得AD2=DGBD，再利用已知条件可证明∠ABD=∠DAG=∠F，进而可得到cosF=cos∠ABG的值．

∵四边形ABCD是菱形，

∴CD=AD，∠CDG=∠ADG，

在△ADG和△CDG中，

，

∴△ADG≌△CDG（SAS），

∴∠DAG=∠DCG，CG=AG

∵BF∥CD，

∴∠F=∠DCG=∠DAG，

∴△GAE∽△GFA，

∴AG2=GEGF，

∴CG2=GEGF；

（2）∵BF∥CD，DG=GB，

∴，

∴BF=2CD=16，AF=8，

∴∠ABD=∠DAG=∠F，

∴△DAG∽△DBA，

∴AD2=DGBD，

∴DG=，BG=，

∴cosF=cos∠ABG=．