��Ŀ����
����Ŀ����ͼ����֪���κ���y=ax2+bx+c����A����1��0����B��3��0����N��2��3�����㣬����y�ύ�ڵ�C��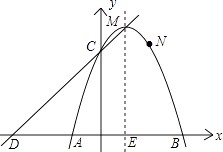
��1����������κ����Ľ���ʽ����д������M����C�����ꣻ
��2����ֱ��y=kx+d����C��M���㣬����x�ύ�ڵ�D����֤���ı���CDAN��ƽ���ı��Σ�
��3����P��������κ����ĶԳ�����һ���㣬��̽�����Ƿ���������ĵ�P��ʹ�Ե�PΪԲ�ĵ�Բ����A��B���㣬������ֱ��CD���У�������ڣ��������P�����ꣻ��������ڣ���˵�����ɣ�
���𰸡�
��1��
�⣺��Ϊ���κ���y=ax2+bx+c��ͼ����A����1��0����B��3��0����N��2��3��
���ԣ��ɽ��������飺 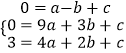 ����ã�
����ã� ![]()
���ԣ�������κ����Ľ���ʽΪy=��x2+2x+3��
���ԣ�����M��1��4������C��0��3��
��2��
�⣺ֱ��y=kx+d����C��M���㣬
���� ![]() ��
��
��k=1��d=3��
ֱ�߽���ʽΪy=x+3��
��y=0����x=��3��
��D����3��0��
��CD= ![]() ��AN=
��AN= ![]() ��AD=2��CN=2
��AD=2��CN=2
��CD=AN��AD=CN��2�֣�
���ı���CDAN��ƽ���ı���
��3��
�⣺������������ĵ�P��ʹ�Ե�PΪԲ�ĵ�Բ����A��B���㣬������ֱ��CD���У�
��Ϊ������κ����ĶԳ�����ֱ��x=1��
�ʿ���P��1��y0����
��PA��Բ�İ뾶��PA2=y02+22��
��P��ֱ��CD�Ĵ��ߣ�����ΪQ����PQ=PAʱ��PΪԲ�ĵ�Բ��ֱ��CD���У�
�ɵڣ�2��С���ã���MDEΪ����ֱ�������Σ�
�ʡ�PQMҲ�ǵ���ֱ�������Σ�
��P��1��y0����PE=y0��PM=|4��y0|�� ![]() ��
��
��PQ2=PA2�÷��̣� ![]() ��
��
��� ![]() ���������⣬
���������⣬
���ԣ���������ĵ�P���ڣ�������Ϊ��1�� ![]() ����1��
����1�� ![]() ��
��
����������1���������⽫��A��B��N��������뺯������ʽ����ɷ����鼴����ã���2����õ�C��M�����꣬�ɵ�ֱ��CM�Ľ���ʽ������õ�D�����꣬���ɵõ�CD= ![]() ��AN=
��AN= ![]() ��AD=2��CN=2������ƽ���ı��ε��ж������ɵ��ı���CDAN��ƽ���ı��Σ���3��������������ĵ�P��ʹ�Ե�PΪԲ�ĵ�Բ����A��B���㣬������ֱ��CD���У���Ϊ������κ����ĶԳ�����ֱ��x=1���ʿ���P��1��y0������PA��Բ�İ뾶��PA2=y02+22 ��
��AD=2��CN=2������ƽ���ı��ε��ж������ɵ��ı���CDAN��ƽ���ı��Σ���3��������������ĵ�P��ʹ�Ե�PΪԲ�ĵ�Բ����A��B���㣬������ֱ��CD���У���Ϊ������κ����ĶԳ�����ֱ��x=1���ʿ���P��1��y0������PA��Բ�İ뾶��PA2=y02+22 ��
��P��ֱ��CD�Ĵ��ߣ�����ΪQ����PQ=PAʱ��PΪԲ�ĵ�Բ��ֱ��CD���У�
�ɵڣ�2��С���ã���MDEΪ����ֱ�������Σ��ʡ�PQMҲ�ǵ���ֱ�������Σ��̶������������ĵ�P���ڣ�������Ϊ��1�� ![]() ����1��
����1�� ![]() ����
����
�����㾫����������Ŀ����֪���������ö��κ��������ʵ����֪ʶ���Եõ�����Ĵ𰸣���Ҫ���������ԣ���a>0ʱ���Գ�����ߣ�y��x�������С���Գ����ұߣ�y��x���������a<0ʱ���Գ�����ߣ�y��x��������Գ����ұߣ�y��x�������С��

 ��ĩ1�����ʽ���������ϵ�д�
��ĩ1�����ʽ���������ϵ�д�