题目内容
【题目】我们规定,若关于![]() 的一元一次方程
的一元一次方程![]() 的解为
的解为![]() ,则称该方程为“奇异方程”.例如:
,则称该方程为“奇异方程”.例如:![]() 的解为
的解为![]() ,则该方程
,则该方程![]() 是“奇异方程”.请根据上述规定解答下列问题:
是“奇异方程”.请根据上述规定解答下列问题:
(Ⅰ)判断方程![]() ________(回答“是”或“不是”)“奇异方程”;
________(回答“是”或“不是”)“奇异方程”;
(Ⅱ)若![]() ,有符合要求的“奇异方程”吗?若有,求
,有符合要求的“奇异方程”吗?若有,求![]() 的值;若没有,请说明理由.
的值;若没有,请说明理由.
(Ⅲ)若关于![]() 的一元一次方程
的一元一次方程![]() 和
和![]() 都是“奇异方程”,求代数式
都是“奇异方程”,求代数式![]() +
+![]()
![]() 的值.
的值.
【答案】(Ⅰ)不是;(Ⅱ)![]() 时有符合要求的“奇异方程”;(Ⅲ)
时有符合要求的“奇异方程”;(Ⅲ)![]() .
.
【解析】
(Ⅰ)解方程,并计算对应b-a的值与方程的解不相等,所以不是奇异方程;
(Ⅱ)根据奇异方程的定义即可得出关于b的方程,解方程即可;
(Ⅲ)根据奇异方程的概念列式得到关于m、n的两个方程,联立求解得到m、n的关系,然后代入化简后的代数式进行计算即可求解.
(Ⅰ):∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
![]() ,
,
∴![]() 不是奇异方程;
不是奇异方程;
故答案为:不是;
(Ⅱ)∵![]() ,
,
∴3x=b,解得,x=![]()
若方程3x=b有符合要求的“奇异方程”
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
即![]() 时有符合要求的“奇异方程”;
时有符合要求的“奇异方程”;
(Ⅲ)关于![]() 的一元一次方程
的一元一次方程![]() 和
和![]() 都是“奇异方程”,则有:
都是“奇异方程”,则有:
![]() ,
,![]()
整理得:![]() ,
,![]() ,
,
两式相减得,![]() ,
,
∴![]()
![]() ,
,
![]()
![]() ,
,
![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】甲、乙两名射击选手在10次射击训练中的成绩统计图(部分)如图所示:
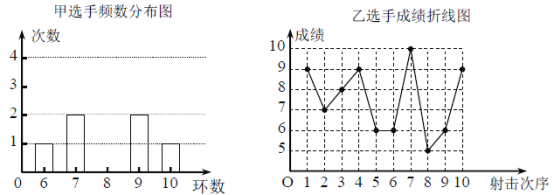
教练根据甲、乙两名射击选手的成绩绘制了如下数据分析表:
选手 | 平均数 | 中位数 | 众数 | 方差 |
甲 |
| 8 | 8 | c |
乙 | 7. 5 |
| 6和9 | 2. 65 |
根据以上信息,请解答下面的问题:
(1)补全甲选手10次成绩频数分布图;
(2)求![]() 的值;
的值;
(3)教练根据两名选手的10次成绩,决定选择甲选手参加射击比赛,教练的理由是什么?(至少从两个不同角度说明理由).