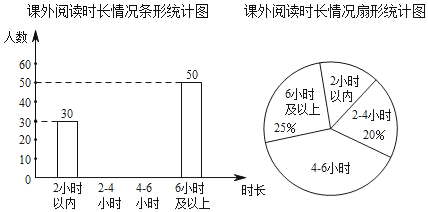
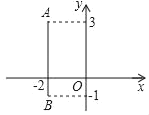
��Ŀ����
����Ŀ���ס���������һ����ֱ�ĵ�·��������У��������г���A�ص�B�أ��Ҽݳ���B�ص�A�أ����Ƿֱ��Բ�ͬ���ٶ�������ʻ����֪���ȳ���6���Ӻ��Ҳų����������������У��ס������˵ľ���y��ǧ�ף���׳�����ʱ��x���֣�֮��Ĺ�ϵ��ͼ��ʾ��
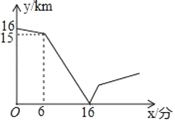
��1�����ٶ�Ϊ�� ��ǧ��/�֣���������ʱ���������� �����ӣ��ҵ��ٶ�Ϊ�� ��ǧ��/�֣�
��2������ҳ�������������ʱ��y��x�ĺ�����ϵʽ��
��3���ҵ���A��ʱ�������� �����ӵ�����B�أ�
���𰸡���1��24��10��![]() ����2��y��
����2��y��![]() ����3��78
����3��78
��������
��1������ͼ�εó����ٶȣ��ٵó��ҵ�ʱ�䣬���ҵ��ٶ���xǧ��/���ӣ����������г����̣����ɽ��.
��2����y��x�ĺ�����ϵʽΪy��kx+b������������������������г�������.
�⣺��1���۲�ͼ��֪A��B�������Ϊ16km��
������ʻ��1ǧ�ף��ɺ����꿴������ʻ1ǧ������6���ӣ�
����ٶ���![]() ǧ��/���ӣ�
ǧ��/���ӣ�
�������꿴�������ˣ�16��6��10���֣���
���ҵ��ٶ���xǧ��/���ӣ������⣬��
10x+16��![]() ��16��
��16��
���x��![]() ��
��
���ҵ��ٶ�Ϊ![]() ǧ��/���ӣ�
ǧ��/���ӣ�
�ʴ�Ϊ��24��10��![]() ��
��
��2����y��x�ĺ�����ϵʽΪy��kx+b����������ã�
![]() �����
�����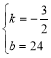 ��
��
��y��![]() ��
��
��3���������ҵ���Aվ���裨16��![]() ����
����![]() ��
��![]() ��ǧ�ף�
��ǧ�ף�
�������ҵ���Aվ���裨16��![]() ����
����![]() ��2�����ӣ���
��2�����ӣ���
���������Bվ���裨10��![]() ����
����![]() ��80���ӣ�
��80���ӣ�
���ҵ����յ�Aʱ������80��2��78���ӵ����յ�B��
�ʴ�Ϊ��78��