ЬтФПФкШн
ЁОЬтФПЁПвбжЊХзЮяЯпyЃНax2Ѓ2amxЃЋam2ЃЋ2mЃЋ4ЕФЖЅЕуPдквЛЬѕЖЈжБЯпlЩЯЃЎ
ЃЈ1ЃЉжБНгаДГіжБЯпlЕФНтЮіЪНЃЛ
ЃЈ2ЃЉШєДцдкЮЈвЛЕФЪЕЪ§mЃЌЪЙХзЮяЯпОЙ§дЕуЃЎ
ЂйЧѓДЫЪБЕФaКЭmЕФжЕЃЛ
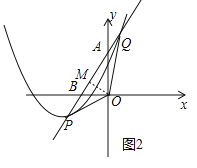
ЂкХзЮяЯпЕФЖдГЦжсгыxжсНЛгкЕуAЃЌBЮЊХзЮяЯпЩЯвЛЖЏЕуЃЌвдOAЁЂOBЮЊБпзїЁѕOACBЃЌШєЕуCдкХзЮяЯпЩЯЃЌЧѓBЕФзјБъЃЎ
ЃЈ3ЃЉХзЮяЯпгыжБЯпlЕФСэвЛИіНЛЕуQЃЌШєaЃН1ЃЌжБНгаДГіЁїOPQЕФУцЛ§ЕФжЕЛђШЁжЕЗЖЮЇЃЎ
ЁОД№АИЁПЃЈ1ЃЉy=2x+4ЃЈ2ЃЉЂйm=-4ЃЛЂкBЃЈ-2ЃЌ-3ЃЉЃЈ3ЃЉ![]()
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉРћгУХфЗНЗЈЧѓГіЖЅЕузјБъЃЌМДПЩНтОіЮЪЬтЃЎ
ЃЈ2ЃЉЂйХзЮяЯпОЙ§дЕуЃЌЫљвдx=0ЪБЃЌy=0ЃЌЕУam2+2m+4=0ЃЌвђЮЊЪЕЪ§mЮЈвЛЃЌЫљвдЁї=0ЃЌЕУЕН4Љ16a=0ЃЌПЩЕУa=![]() ЃЌm=Љ4ЃЎ
ЃЌm=Љ4ЃЎ
ЂкШчЭМ1жаЃЌИљОнЦНааЫФБпаЮЕФаджЪЃЌПЩжЊЕуBЕФКсзјБъЮЊЉ2ЃЌгЩДЫПЩвдЧѓГіЕуBзјБъЃЎ
ЃЈ3ЃЉШчЭМ2жаЃЌжБЯпy=2x+4гыxжсНЛгкЕуBЃЈЉ2ЃЌ0ЃЉЃЌНЛyжсгкЕуAЃЈ0ЃЌ4ЃЉЃЌзїOMЁЭABгкMЃЎгЩ![]() OAOB=
OAOB=![]() ABOMЃЌЧѓГіOMЃЌРћгУЗНГЬзщ
ABOMЃЌЧѓГіOMЃЌРћгУЗНГЬзщ![]() ЃЌПЩЕУPЃЈmЃЌm+2ЃЉЃЌQЃЈm+2ЃЌ2m+8ЃЉЃЌЧѓГіPQЕФГЄМДПЩНтОіЮЪЬтЃЎ
ЃЌПЩЕУPЃЈmЃЌm+2ЃЉЃЌQЃЈm+2ЃЌ2m+8ЃЉЃЌЧѓГіPQЕФГЄМДПЩНтОіЮЪЬтЃЎ
ЪдЬтНтЮіЃКНтЃКЃЈ1ЃЉЁпy=ax2Љ2amx+am2+2m+4=aЃЈxЉmЃЉ2+2m+4ЃЌЁрЖЅЕуPзјБъЮЊЃЈmЃЌ2m+4ЃЉЃЌЁрЖЅЕуPдкжБЯпy=2x+4ЩЯЃЎ
ЃЈ2ЃЉЂйЁпХзЮяЯпОЙ§дЕуЃЌЁрx=0ЪБЃЌy=0ЃЌЁрam2+2m+4=0ЃЌЁпЪЕЪ§mЮЈвЛЃЌЁрЁї=0ЃЌЁр4Љ16a=0ЃЌЁрa=![]() ЃЌm=Љ4ЃЎ
ЃЌm=Љ4ЃЎ
ЂкШчЭМ1жаЃЌЁпЫФБпаЮOACBЪЧЦНааЫФБпаЮЃЌЁрOAЁЮBCЃЌOA=BC=4ЃЌЁпBCЁЮxжсЃЌAЃЈЉ4ЃЌ0ЃЉЃЌИљОнЖдГЦадПЩжЊЃЌBЁЂCЙигкЖдГЦжсЖдГЦЃЌЁрЕуBЕФКсзјБъЮЊЉ2ЃЌy=![]() ЃЈx+4ЃЉ2Љ4ЃЌЁрx=Љ2ЪБЃЌy=Љ3ЃЌЁрЕуBзјБъЮЊЃЈЉ2ЃЌЉ3ЃЉЃЎ
ЃЈx+4ЃЉ2Љ4ЃЌЁрx=Љ2ЪБЃЌy=Љ3ЃЌЁрЕуBзјБъЮЊЃЈЉ2ЃЌЉ3ЃЉЃЎ
ЃЈ3ЃЉШчЭМ2жаЃЌЁпжБЯпy=2x+4гыxжсНЛгкЕуBЃЈЉ2ЃЌ0ЃЉЃЌНЛyжсгкЕуAЃЈ0ЃЌ4ЃЉЃЌзїOMЁЭABгкMЃЌЁрOB=2ЃЌOA=4ЃЌЁрAB=![]() =
=![]() ЃЎЁп
ЃЎЁп![]() OAOB=
OAOB=![]() ABOMЃЌЁрOM=/span>
ABOMЃЌЁрOM=/span>![]() ЃЎЁпa=1ЃЌЁрХзЮяЯпЕФНтЮіЪНЮЊy=x2Љ2mx+m2+2m+4ЃЌгЩ
ЃЎЁпa=1ЃЌЁрХзЮяЯпЕФНтЮіЪНЮЊy=x2Љ2mx+m2+2m+4ЃЌгЩ![]() ЃЌЯћШЅyЕУx2ЉЃЈ2m+2ЃЉx+mЃЈm+2ЃЉ=0ЃЌНтЕУx=mЛђm=2ЃЌЁр
ЃЌЯћШЅyЕУx2ЉЃЈ2m+2ЃЉx+mЃЈm+2ЃЉ=0ЃЌНтЕУx=mЛђm=2ЃЌЁр![]() Лђ
Лђ![]() ЃЌЁрPЃЈmЃЌm+2ЃЉЃЌQЃЈm+2ЃЌ2m+8ЃЉЃЌЁрPQ=
ЃЌЁрPЃЈmЃЌm+2ЃЉЃЌQЃЈm+2ЃЌ2m+8ЃЉЃЌЁрPQ=![]() =
=![]() ЃЌЁрSЁїPOQ=
ЃЌЁрSЁїPOQ=![]() PQOM=
PQOM=![]() ЁС
ЁС![]() ЁС
ЁС![]() =
=![]() ЃЎ
ЃЎ