题目内容
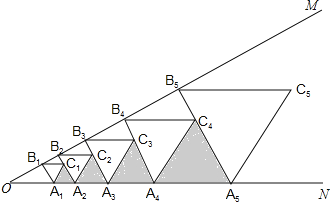
【题目】如图,∠MON=30°,点B1在边OM上,且OB1=2,过点B1作B1A1⊥OM交ON于点A1,以A1B1为边在A1B1右侧作等边三角形A1B1C1;过点C1作OM的垂线分别交OM、ON于点B2、A2,以A2B2为边在A2B2的右侧作等边三角形A2B2C2;过点C2作OM的垂线分别交OM、ON于点B3、A3,以A3B3为边在A3B3的右侧作等边三角形A3B3C3,…;按此规律进行下去,则△AnBn+1Cn的面积为__.(用含正整数n的代数式表示)
【答案】(![]() )2n﹣2×
)2n﹣2×![]()
【解析】由题意△A1A2C1是等边三角形,边长为![]() ,△A2A3C2是等边三角形,边长为
,△A2A3C2是等边三角形,边长为![]() ×
×![]() ,△A3A4C3是等边三角形,边长为
,△A3A4C3是等边三角形,边长为![]() ×
×![]() ×
×![]() =(
=(![]() )2×
)2×![]() ,继而得到△AnBn+1Cn的边长为(
,继而得到△AnBn+1Cn的边长为(![]() )n﹣1×
)n﹣1×![]() ,然后根据等边三角形面积公式进行求解即可得.
,然后根据等边三角形面积公式进行求解即可得.
由题意△A1A2C1是等边三角形,边长为![]() ,
,
△A2A3C2是等边三角形,边长为![]() ×
×![]() ,
,
△A3A4C3是等边三角形,边长为![]() ×
×![]() ×
×![]() =(
=(![]() )2×
)2×![]() ,
,
△A4A5C4是等边三角形,边长为![]() ×
×![]() ×
×![]() ×
×![]() =(
=(![]() )3×
)3×![]() ,
,
…,
△AnBn+1Cn的边长为(![]() )n﹣1×
)n﹣1×![]() ,
,
∴△AnBn+1Cn的面积为![]() ×[(
×[(![]() )n﹣1×
)n﹣1×![]() ]2=(
]2=(![]() )2n﹣2×
)2n﹣2×![]() ,
,
故答案为:(![]() )2n﹣2×
)2n﹣2×![]() .
.

练习册系列答案
相关题目
【题目】股市一周内周六、周日两天不开市,股民小王上周五以每股25.20元的价格买进某公司股票10000股,下表为本周内每天该股票的涨跌情况:
星期 | 一 | 二 | 三 | 四 | 五 |
每股涨 跌情况 | -0.1 | +0.4 | -0.2 | -0.4 | +0.5 |
注:表中正数表示股价比前一天上涨,负数表示股价比前一天下跌.
(1)星期四收盘时,每股多少元?
(2)本周内哪一天股价最高,是多少元?
(3)股民小王本周末将该股票全部售出(不记交易税),小王在本次交易中获利多少元?