题目内容
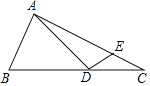
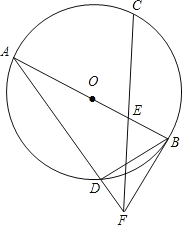
【题目】如图,AB是⊙O的直径,![]() ,E是OB的中点,连接CE并延长到点F,使EF=CE.连接AF交⊙O于点D,连接BD,BF.
,E是OB的中点,连接CE并延长到点F,使EF=CE.连接AF交⊙O于点D,连接BD,BF.
(1)求证:直线BF是⊙O的切线;
(2)若OB=2,求BD的长.
【答案】(1)证明见解析;(2)BD=![]() .
.
【解析】(1)连接OC,由已知可得∠BOC=90°,根据SAS证明△OCE≌△BFE,根据全等三角形的对应角相等可得∠OBF=∠COE=90°,继而可证明直线BF是⊙O的切线;
(2),由(1)的全等可知BF=OC=2,利用勾股定理求出AF的长,然后由S△ABF=![]() ,即可求出BD=
,即可求出BD=![]() .
.
(1)连接OC,
∵AB是⊙O的直径,![]() ,∴∠BOC=90°,
,∴∠BOC=90°,
∵E是OB的中点,∴OE=BE,
在△OCE和△BFE中,
 ,
,
∴△OCE≌△BFE(SAS),
∴∠OBF=∠COE=90°,
∴直线BF是⊙O的切线;
(2)∵OB=OC=2,由(1)得:△OCE≌△BFE,
∴BF=OC=2,
∴AF=![]() ,
,
∴S△ABF=![]() ,
,
即4×2=2![]() BD,
BD,
∴BD=![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目