Question

【题目】在平面直角坐标系中，点A、B、C的坐标分别为，，，点P，Q是边上的两个动点点P不与点C重合，以P，O，Q为顶点的三角形与全等，则满足条件的点P的坐标为______．

Answer 1

【答案】或

【解析】

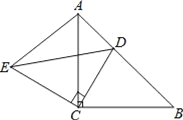
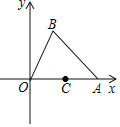
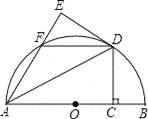
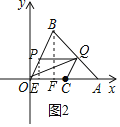
如图1所示，当≌时，即，过P作于E，过B作于F，则，根据勾股定理得到，根据相似三角形的性质得到，，于是得到点P的坐标为；如图2，当≌时，即，，点的四边PQCO是平行四边形，求得，过P作于E，过B作于F，则，根据平行线分线段成比例定理即可得到结论．

以P，O，Q为顶点的三角形与全等，

如图1所示，当≌时，

即，

过P作于E，过B作于F，

则，

，

，，

，

，

∽，

，

，

，，

点P的坐标为；

如图2，当≌时，

即，，

四边形PQCO是平行四边形，

，

过P作于E，过B作于F，

则，

，

，，

，

，

，

，

，

点P是OB的中点，

，

，，

点P的坐标为，

综上所述，点P的坐标为或．

故答案为：或．