题目内容
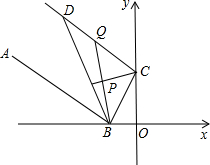
如图,AB、CD是半径为1的⊙P两条直径,且∠CPB=120°,⊙M与PC、PB及弧CQB都相切,O、 Q分别为PB、弧CQB上的切点.
Q分别为PB、弧CQB上的切点.(1)试求⊙M的半径r;
(2)以AB为x轴,OM为y轴(分别以OB、OM为正方向)建立直角坐标系,
①设直线y=kx+m过点M、Q,求k,m;?????????????????
②设函数y=x2+bx+c的图象经过点Q、O,求此函数解析式;
③当y=x2+bx+c<0时,求x的取值范围;
④若直线y=kx+m与抛物线y=x2+bx+c的另一个交点为E,求线段EQ的长度.
分析:(1)利用在Rt△POM中
=sin60°=
与PQ=PM+MQ建立起⊙P半径与⊙M半径r间的关系,从而求得r的值.
(2)①首先根据半径r与∠QPB=60°确定出M、Q两点的坐标,再代入y=kx+m,解方程求得k、m的值.
②首先根据y=x2+bx+c的图象经过点O,确定出c=0,再将Q点的坐标代入y=x2+bx+c,求得b的值,此函数解析式确定.
③将抛物线y=x2+bx+c首先转化为一元二次方程x2+bx+c=0的值x1、x2(其中x1≤x2)的值,那么y=x2+bx+c<0关于x的取值范围即为x1<x<x2.
④通过上面①②知两解析式分别是y=
x+2
-3、y=x2+
x首先求得E点坐标,Q点的坐标通过图不难确定,那么再求的两点间的距离即可.
| r |
| PM |
| ||
| 2 |
(2)①首先根据半径r与∠QPB=60°确定出M、Q两点的坐标,再代入y=kx+m,解方程求得k、m的值.
②首先根据y=x2+bx+c的图象经过点O,确定出c=0,再将Q点的坐标代入y=x2+bx+c,求得b的值,此函数解析式确定.
③将抛物线y=x2+bx+c首先转化为一元二次方程x2+bx+c=0的值x1、x2(其中x1≤x2)的值,那么y=x2+bx+c<0关于x的取值范围即为x1<x<x2.
④通过上面①②知两解析式分别是y=
| 3 |
| 3 |
| 7 |
| 2 |
解答: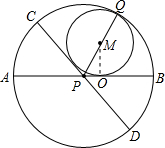 解:(1)由
解:(1)由
=sin60°=
,PM+MQ=
+r=1,
得r=2
-3.(2分)
(2)①点M(0,r),即M(0,2
-3);
点Q(rcos60°,
),即Q(
-
,
).
由已知直线过点M、Q,得m=2
-3,k(
-
)+m=
,
解得k=
,m=2
-3. (5分)
②由y=x2+bx+c过点O、Q,则c=0,
(
)2+b(
)=
,得b=
,
即得y=x2+
x.(8分)
③令x2+
x=0,则x1=-
,x2=0,
即得当-
<x<0时,y<0.
④由已知得y=
x+2
-3,y=x2+
x,
消去y,得x2+(
-
)x+3-2
=0. (12分)
设点E的横坐标为x2,点Q的横坐标为x1=
-
,
由根与系数的关系得x2=-2,
则|x1-x2|=|
-
+2|=
+
(14分)
进而得线段EQ的长为2
+1. (15分)
 解:(1)由
解:(1)由| r |
| PM |
| ||
| 2 |
| 2r | ||
|
得r=2
| 3 |
(2)①点M(0,r),即M(0,2
| 3 |
点Q(rcos60°,
| ||
| 2 |
| 3 |
| 3 |
| 2 |
| ||
| 2 |
由已知直线过点M、Q,得m=2
| 3 |
| 3 |
| 3 |
| 2 |
| ||
| 2 |
解得k=
| 3 |
| 3 |
②由y=x2+bx+c过点O、Q,则c=0,
(
2
| ||
| 2 |
2
| ||
| 2 |
| ||
| 2 |
| 7 |
| 2 |
即得y=x2+
| 7 |
| 2 |
③令x2+
| 7 |
| 2 |
| 7 |
| 2 |
即得当-
| 7 |
| 2 |
④由已知得y=
| 3 |
| 3 |
| 7 |
| 2 |
消去y,得x2+(
| 7 |
| 2 |
| 3 |
| 3 |
设点E的横坐标为x2,点Q的横坐标为x1=
| 3 |
| 3 |
| 2 |
由根与系数的关系得x2=-2,
则|x1-x2|=|
| 3 |
| 3 |
| 2 |
| 3 |
| 1 |
| 2 |
进而得线段EQ的长为2
| 3 |
点评:本题主要考查了二次函数解析式的确定、函数图象交点的求法等知识点.主要考查学生数形结合的数学思想方法.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案
相关题目
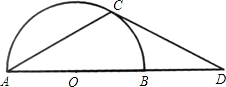 如图,AB是半⊙O的直径,弦AC与AB成30°的角,AC=CD.
如图,AB是半⊙O的直径,弦AC与AB成30°的角,AC=CD.
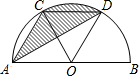 如图,AB是半⊙O的直径,C、D是半圆的三等分点,半圆的半径为R.
如图,AB是半⊙O的直径,C、D是半圆的三等分点,半圆的半径为R. (2012•武汉模拟)如图,AB为⊙O的直径,AM和BN是它的两条切线,E为⊙O的半圆弧上一动点(不与A、B重合),过点E的直线分别交射线AM、BN于D、C两点,且CB=CE.
(2012•武汉模拟)如图,AB为⊙O的直径,AM和BN是它的两条切线,E为⊙O的半圆弧上一动点(不与A、B重合),过点E的直线分别交射线AM、BN于D、C两点,且CB=CE.