Question

【题目】如图，抛物线C1：y＝x2﹣2x﹣3与x轴交于A、B两点，点A在点B的左侧，将抛物线C1向上平移1个单位得到抛物线C2，点Q（m，n）在抛物线C2上，其中m＞0且n＜0，过点P作PQ∥y轴交抛物线C1于点P，点M是x轴上一点，当以点P、Q、M为顶点的三角形与△AOQ全等时，点M的横坐标为_____．

Answer 1

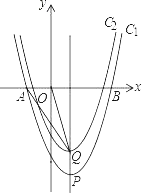
【答案】4

【解析】

此题首先需要确定全等的对应关系，函数图象向上平移后，两个函数上下间距为1，OA＝1，所以AO与PQ对应，∠AOQ＝∠PQM，可确定OQ＝QM，AQ＝PB，得到两组线段相等后，设点M坐标，以两组线段相等为等量建立方程即可解决问题．

解：∵△AOQ≌△PQM，AO＝PQ

∴∠AOQ＝∠PQM，AQ＝PB，OQ＝QM

∴AQ2＝PB2，OQ2＝QM2

设Q（m，m2﹣2m﹣2），P（m，m2﹣2m﹣3），M（a，0）

如图，过点Q作QH⊥AB，垂足为H，

则在Rt△OHQ中，OQ2＝（m）2+（m2﹣2m﹣2）2；

在Rt△MHQ中，QM2＝（a﹣m）2+（m2﹣2m﹣2）2；

在Rt△AHQ中，AQ2＝（m+1）2+（m2﹣2m﹣2）2；

在Rt△PHB中，PB2＝（a﹣m）2+（m2﹣2m﹣3）2

由（m）2+（m2﹣2m﹣2）2＝（a﹣m）2+（m2﹣2m﹣2）2，解得m＝

由（m+1）2+（m2﹣2m﹣2）2＝（a﹣m）2+（m2﹣2m﹣3）2，解得a＝﹣2（舍）或a＝4

∴点M的横坐标为4．