题目内容
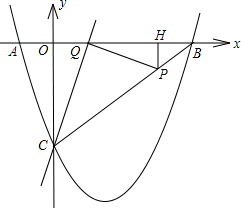 如图,已知抛物线y=
如图,已知抛物线y=| 3 |
| 4 |
| 3 |
| 4t |
(1)确定b,c的值;
(2)求线段QH的长度(用含t的式子表示);
(3)依点P的变化,是否存在t的值,使△COQ与△QPH相似?若存在,求出所有t的值;若不存在,说明理由.
分析:(1)根据直线CQ的解析式可求出C点的坐标,然后将A、C坐标代入抛物线中即可求出b、c的值.
(2)根据(1)得出的抛物线可求出B点的坐标,即可得出∠PBH的三角函数值(通过相似三角形△BHP,△BOC来求也行).已知了BP的坐标,即可根据∠PBH的三角函数求出BH、PH的长,可根据直线CQ的解析式求出OQ的长,那么由QH=OH-OQ或QH=OQ-OH(当H在OQ之间时)即可得出QH的表达式.
(3)本题要分情况进行讨论:
①当Q在OH之间时,此时QH=OH-OQ,可分△OQC∽△HPQ和△OQC∽△HQP两种情况来求,可根据各自的对应成比例线段求出t的值.
②当Q在BH之间时,此时QH=OQ-OH,PH∥OC,只有△QHP∽△QOC一种情况,可根据对应成比例线段求出t的值.
(2)根据(1)得出的抛物线可求出B点的坐标,即可得出∠PBH的三角函数值(通过相似三角形△BHP,△BOC来求也行).已知了BP的坐标,即可根据∠PBH的三角函数求出BH、PH的长,可根据直线CQ的解析式求出OQ的长,那么由QH=OH-OQ或QH=OQ-OH(当H在OQ之间时)即可得出QH的表达式.
(3)本题要分情况进行讨论:
①当Q在OH之间时,此时QH=OH-OQ,可分△OQC∽△HPQ和△OQC∽△HQP两种情况来求,可根据各自的对应成比例线段求出t的值.
②当Q在BH之间时,此时QH=OQ-OH,PH∥OC,只有△QHP∽△QOC一种情况,可根据对应成比例线段求出t的值.
解答: 解:(1)c=-3
解:(1)c=-3
将(-1,0)和c=-3代入y=
x2+bx+c,
得b=-
.
(2)设P坐标为(x,y),由y=
x2-
x-3,
可求得A(-1,0),B(4,0).
由y=
x-3,
可求得Q(4t,0).
由题意可证△BHP∽△BOC,
OB:OC:BC=4:3:5即BH:HP:BP=4:3:5,
BP=5t,则BH=4t=4-x,OH=x=4-4t
而QH=OH-OQ或QH=OQ-OH(当H在OQ之间时)
又因为OQ=4t,BH=4t
所以,QH=4-4t-4t或QH=4t-(4-4t)
即QH=4-8t或8t-4
即QH=|4-8t|.
(3)存在这样的t的值使△COQ与△QPH相似,
当QH=OH-OQ=4-8t时,PH=3t,OQ=4t,OC=3,QH=4-8t,
若相似,则QH:OC=3:4,
所以t=
,
当QH=OQ-OH=8t-4时,PH=3t,OQ=4t,OC=3,QH=8t-4,
若相似,则QH:OC=3:4,
所以t=
,
当QH=OH-OQ=4-8t时,OQ:QH=OC:PH,
得
=
,t2+2t-1=0
所以t1=
-1,t2=-
-1(舍去)
综上,存在t的值,t的值为
或
或
-1.
 解:(1)c=-3
解:(1)c=-3将(-1,0)和c=-3代入y=
| 3 |
| 4 |
得b=-
| 9 |
| 4 |
(2)设P坐标为(x,y),由y=
| 3 |
| 4 |
| 9 |
| 4 |
可求得A(-1,0),B(4,0).
由y=
| 3 |
| 4t |
可求得Q(4t,0).
由题意可证△BHP∽△BOC,
OB:OC:BC=4:3:5即BH:HP:BP=4:3:5,
BP=5t,则BH=4t=4-x,OH=x=4-4t
而QH=OH-OQ或QH=OQ-OH(当H在OQ之间时)
又因为OQ=4t,BH=4t
所以,QH=4-4t-4t或QH=4t-(4-4t)
即QH=4-8t或8t-4
即QH=|4-8t|.
(3)存在这样的t的值使△COQ与△QPH相似,
当QH=OH-OQ=4-8t时,PH=3t,OQ=4t,OC=3,QH=4-8t,
若相似,则QH:OC=3:4,
所以t=
| 7 |
| 32 |
当QH=OQ-OH=8t-4时,PH=3t,OQ=4t,OC=3,QH=8t-4,
若相似,则QH:OC=3:4,
所以t=
| 25 |
| 32 |
当QH=OH-OQ=4-8t时,OQ:QH=OC:PH,
得
| 4t |
| 4-8t |
| 3 |
| 3t |
所以t1=
| 2 |
| 2 |
综上,存在t的值,t的值为
| 7 |
| 32 |
| 25 |
| 32 |
| 2 |
点评:本题考查了二次函数解析式的确定以及相似三角形的判定和性质等知识点.
要注意的是(3)中要根据Q的位置和不同的对应相似三角形来分类求解.不要漏解.
要注意的是(3)中要根据Q的位置和不同的对应相似三角形来分类求解.不要漏解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 C(0,3).
C(0,3). 、C(0,-3)两点,与x轴交于另一点B.
、C(0,-3)两点,与x轴交于另一点B. (2013•衡阳)如图,已知抛物线经过A(1,0),B(0,3)两点,对称轴是x=-1.
(2013•衡阳)如图,已知抛物线经过A(1,0),B(0,3)两点,对称轴是x=-1. 如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,且抛物线经过A(-1,0)、C(0,-3)两点,与x轴交于另一点B.
如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,且抛物线经过A(-1,0)、C(0,-3)两点,与x轴交于另一点B. 如图,已知抛物线y=ax2+bx+c的顶点是(-1,-4),且与x轴交于A、B(1,0)两点,交y轴于点C;
如图,已知抛物线y=ax2+bx+c的顶点是(-1,-4),且与x轴交于A、B(1,0)两点,交y轴于点C;