题目内容
【题目】如图,在△ABC中,AD⊥BC,BE⊥AC,AD、BE相交于点![]() ,且BF=AC.
,且BF=AC.
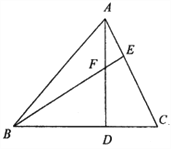
(1)求证:△ADC≌△BDF
(2)若CD=3,BD=5,求AF的长.
【答案】(1)证明见解析;(2)AF=2.
【解析】(1)先证明AD=BD,再证明∠FBD=∠DAC,从而利用ASA证明△BDF≌△ADC;
(2)利用全等三角形对应边相等得出DF=CD=4,根据勾股定理求出CF即可.
解:(1)证明:∵AD⊥BC,BE⊥AC,
∴∠FDB=∠CDA=∠AEF=90°.
∵∠FBD+∠FDB+∠BFD=180°,
∠CAD+∠AEF+∠AFE=180°,
又∵∠BFD=∠AFE,
∴ ∠FBD = ∠CAD.
∵在△ADC和△BDF中,
∠FDB=∠CDA ,
∠FBD = ∠CAD ,
BF=AC,
∴ △ADC≌△BDF(AAS).
(2) 解:∵ 由(1)知,
△ADC≌△BDF,
∴ DC=DF,AD=BD,
∴ AF=AD-DF=BD-CD=5-3=2.
“点睛”此题主要考查了全等三角形的判定和性质,勾股定理的应用,关键是找出能使三角形全等的条件,注意:全等三角形的判定定理有SAS、ASA、AAS、SSS,全等三角形的对应角相等,对应边相等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
