题目内容
在复习《反比例函数》一课时，同桌的小峰和小轩有一个问题观点不一致：
情境：随机同时掷两枚质地均匀的骰子（骰子六个面上的点数分别代表1，2，3，4，5，6）．第一枚骰子上的点数作为点P（m，n）的横坐标，第二枚骰子上的点数作为P（m，n）的纵坐标．
小峰认为：点P（m，n）在反比例函数y=
图象上的概率一定大于在反比例函数y=
图象上的概率；
小轩认为：P（m，n）在反比例函数y=和y=图象上的概率相同．
问题：（1）试用列表或画树状图的方法，列举出所有点P（m，n）的情形；
（2）分别求出点P（m，n）在两个反比例函数的图象上的概率，并说明谁的观点正确．
解：（1）列表得：
画树状图：
．
（2）一共有36种可能的结果，且每种结果的出现可能性相同，
点（2，4），（4，2）在反比例函数y=的图象上，
点（1，6），（2，3），（3，2），（6，1）在反比例函数y=的图象上，
则点P（m，n）在在反比例函数y=的图象上的概率为
，
在反比例函数y=的图象上的概率都为：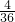
=
，
故两人的观点都不正确．
分析：（1）分别利用列表法以及画树状图列举出所有可能即可；
（2）利用反比例函数图象上点的性质，以及概率公式求出判断谁的观点正确即可．
点评：此题主要考查了列表法求概率问题以及反比例函数图象上点的坐标性质；用到的知识点为：概率等于所求情况数与总情况数之比．
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | （1，1） | （1，2） | （1，3） | （1，4） | （1，5） | （1，6） |
| 2 | （2，1） | （2，2） | （2，3） | （2，4） | （2，5） | （2，6） |
| 3 | （3，1） | （3，2） | （3，3） | （3，4） | （3，5） | （3，6） |
| 4 | （4，1） | （4，2） | （4，3） | （4，4） | （4，5） | （4，6） |
| 5 | （5，1） | （5，2） | （5，3） | （5，4） | （5，5） | （5，6） |
| 6 | （6，1） | （6，2） | （6，3） | （6，4） | （6，5） | （6，6） |
．（2）一共有36种可能的结果，且每种结果的出现可能性相同，
点（2，4），（4，2）在反比例函数y=
的图象上，点（1，6），（2，3），（3，2），（6，1）在反比例函数y=
的图象上，则点P（m，n）在在反比例函数y=
的图象上的概率为，在反比例函数y=
的图象上的概率都为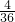：=，故两人的观点都不正确．
分析：（1）分别利用列表法以及画树状图列举出所有可能即可；
（2）利用反比例函数图象上点的性质，以及概率公式求出判断谁的观点正确即可．
点评：此题主要考查了列表法求概率问题以及反比例函数图象上点的坐标性质；用到的知识点为：概率等于所求情况数与总情况数之比．
练习册系列答案
高中必刷题系列答案
相关题目
的横坐标，第二个数作为点
的的图象上的概率一定大于在反比例函数
的图象上的概率，而小芳却认为两者的概率相同．你赞成谁的观点？
的横坐标，第二个数作为点
的的图象上的概率一定大于在反比例函数
的图象上的概率，而小芳却认为两者的概率相同．你赞成谁的观点？