题目内容
 如图,有下列判定:
如图,有下列判定:
①若∠1=∠3,AD∥BC,则BD是∠ABC的平分线;
②若AD∥BC,则∠1=∠2=∠3;
③若∠1=∠3,则AD∥BC;
④若∠C+∠3+∠4=180°,则AD∥BC;
其中正确的有
- A.1个
- B.2个
- C.3个
- D.4个
B
分析:①根据平行线的性质及等量代换,即可得到;②根据平行线的性质,判定即可;③根据平行线的判定定理,判定即可;④根据平行线的判定定理,即可证得;
解答: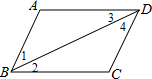 解:①∵AD∥BC,
解:①∵AD∥BC,
∴∠2=∠3,又∠1=∠3,
∴∠1=∠2,
即BD是∠ABC的平分线;故①正确;
②AD∥BC,
∴∠2=∠3,
故②错误;
③∵∠1=∠3,
可得AB=AD,
故③错误;
④若∠C+∠3+∠4=180°,
即∠ADC+∠C=180°,
∴AD∥BC;故④正确;
故选B.
点评:本题主要考查了平行线的判定与性质,解答此题的关键是注意平行线的性质和判定定理的综合运用.
分析:①根据平行线的性质及等量代换,即可得到;②根据平行线的性质,判定即可;③根据平行线的判定定理,判定即可;④根据平行线的判定定理,即可证得;
解答:
 解:①∵AD∥BC,
解:①∵AD∥BC,∴∠2=∠3,又∠1=∠3,
∴∠1=∠2,
即BD是∠ABC的平分线;故①正确;
②AD∥BC,
∴∠2=∠3,
故②错误;
③∵∠1=∠3,
可得AB=AD,
故③错误;
④若∠C+∠3+∠4=180°,
即∠ADC+∠C=180°,
∴AD∥BC;故④正确;
故选B.
点评:本题主要考查了平行线的判定与性质,解答此题的关键是注意平行线的性质和判定定理的综合运用.

练习册系列答案
相关题目
 如图,在下列条件中:①∠1=∠2;②∠BAD=∠BCD;③∠ABC=∠ADC且∠3=∠4;④∠BAD+∠ABC=180°,能判定AB∥CD的有( )
如图,在下列条件中:①∠1=∠2;②∠BAD=∠BCD;③∠ABC=∠ADC且∠3=∠4;④∠BAD+∠ABC=180°,能判定AB∥CD的有( )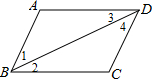 如图,有下列判定:
如图,有下列判定: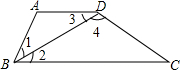 如图,有下列判定,其中正确的有( )
如图,有下列判定,其中正确的有( ) 如图,有下列判定,其中正确的有
如图,有下列判定,其中正确的有