Question

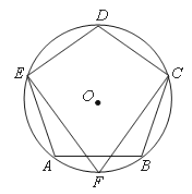
【题目】如图,☉O是正五边形ABCDE的外接圆,F是的中点,连接CF,EF.

(1)请直接写出∠CFE=　 　°;

(2)求证:EF=CF;

(3)若☉O的半径为5,求的长.

Answer 1

【答案】（1）72°；（2）详见解析；（3）3π.

【解析】

（1）根据圆内接四边形的性质和正五边形的内角解答即可；

（2）利用正五边形的性质和弧长关系证明即可；

（3）利用弧长公式解答即可．

解: （1）∵正五边形ABCDE，

∴∠EDC＝108°，

∴∠CFE＝180°108°＝72°，

故答案为：72°.

(2)∵五边形ABCDE是正五边形,∴AE=BC,∴,

又∵F是的中点,∴,

∴,∴,∴EF=CF.

(3)∵☉O是正五边形ABCDE的外接圆,

∴,

∵R=5,∴×2πR=2π,

又∵=π,∴=3π.